". The first part contains the provisions that are minimally necessary for understanding chemometrics, and the second part contains the facts that you need to know for a deeper understanding of the methods of multivariate analysis. The presentation is illustrated by examples made in the Excel workbook Matrix.xls that accompanies this document.

Links to examples are placed in the text as Excel objects. These examples are of an abstract nature; they are in no way tied to the problems of analytical chemistry. Real use cases matrix algebra in chemometrics are discussed in other texts devoted to various chemometric applications.

Most of the measurements carried out in analytical chemistry are not direct but indirect. This means that in the experiment, instead of the value of the desired analyte C (concentration), another value is obtained x(signal) related to but not equal to C, i.e. x(C) ≠ C. As a rule, the type of dependence x(C) is not known, but fortunately in analytical chemistry most measurements are proportional. This means that as the concentration of C in a times, the signal X will increase by the same amount., i.e. x(a C) = a x(C). In addition, the signals are also additive, so that the signal from a sample containing two substances with concentrations C 1 and C 2 will be equal to the sum of the signals from each component, i.e. x(C1 + C2) = x(C1)+ x(C2). Proportionality and additivity together give linearity. Many examples can be given to illustrate the principle of linearity, but it suffices to mention two of the most striking examples - chromatography and spectroscopy. The second feature inherent in the experiment in analytical chemistry is multichannel. Modern analytical equipment simultaneously measures signals for many channels. For example, the intensity of light transmission is measured for several wavelengths at once, i.e. range. Therefore, in the experiment we are dealing with a variety of signals x 1 , x 2 ,...., x n characterizing the set of concentrations C 1 ,C 2 , ..., C m of substances present in the system under study.

Rice. 1 Spectra

So, the analytical experiment is characterized by linearity and multidimensionality. Therefore, it is convenient to consider experimental data as vectors and matrices and manipulate them using the apparatus of matrix algebra. The fruitfulness of this approach is illustrated by the example shown in , which shows three spectra taken for 200 wavelengths from 4000 to 4796 cm–1. First ( x 1) and second ( x 2) the spectra were obtained for standard samples in which the concentrations of two substances A and B are known: in the first sample [A] = 0.5, [B] = 0.1, and in the second sample [A] = 0.2, [B] = 0.6. What can be said about a new, unknown sample, the spectrum of which is indicated x 3 ?

Consider three experimental spectra x 1 , x 2 and x 3 as three vectors of dimension 200. Using linear algebra, one can easily show that x 3 = 0.1 x 1 +0.3 x 2 , so the third sample obviously contains only substances A and B in concentrations [A] = 0.5×0.1 + 0.2×0.3 = 0.11 and [B] = 0.1×0.1 + 0.6×0.3 = 0.19.

1. Basic information

1.1 Matrices

Matrix called a rectangular table of numbers, for example

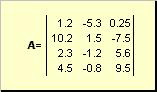
Rice. 2 Matrix

Matrices are denoted by capital bold letters ( A), and their elements - with the corresponding lowercase letters with indices, i.e. a ij . The first index numbers the rows and the second number the columns. In chemometrics, it is customary to denote maximum value index with the same letter as the index itself, but capitalized. Therefore, the matrix A can also be written as ( a ij , i = 1,..., I; j = 1,..., J). For the example matrix I = 4, J= 3 and a 23 = −7.5.

Pair of numbers I and J is called the dimension of the matrix and is denoted as I× J. An example of a matrix in chemometrics is a set of spectra obtained for I samples on J wavelengths.

1.2. The simplest operations with matrices

Matrices can multiply by numbers. In this case, each element is multiplied by this number. For instance -

Rice. 3 Multiplying a matrix by a number

Two matrices of the same dimension can be element-wise fold and subtract. For instance,

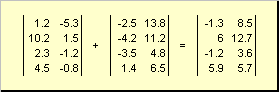
Rice. 4 Matrix addition

As a result of multiplication by a number and addition, a matrix of the same dimension is obtained.

A zero matrix is ​​a matrix consisting of zeros. It is designated O. It's obvious that A+O = A, A−A = O and 0 A = O.

The matrix can transpose. During this operation, the matrix is ​​flipped, i.e. rows and columns are swapped. Transposition is indicated by a dash, A" or index A t . Thus, if A = {a ij , i = 1,..., I; j = 1,...,J), then A t = ( a ji , j = 1,...,J; i = 1,..., I). for instance

Rice. 5 Matrix transposition

It's obvious that ( A t) t = A, (A+B) t = A t+ B t .

1.3. Matrix multiplication

Matrices can multiply, but only if they have the appropriate dimensions. Why this is so will be clear from the definition. Matrix product A, dimension I× K, and matrices B, dimension K× J, is called the matrix C, dimension I× J, whose elements are numbers

Thus for the product AB it is necessary that the number of columns in the left matrix A was equal to the number of rows in the right matrix B. Matrix product example -

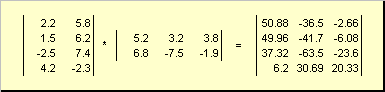
Fig.6 Product of matrices

The matrix multiplication rule can be formulated as follows. To find an element of a matrix C standing at the intersection i-th line and j-th column ( c ij) must be multiplied element by element i-th row of the first matrix A on the j-th column of the second matrix B and add up all the results. So in the example shown, the element from the third row and the second column is obtained as the sum of the element-wise products of the third row A and second column B

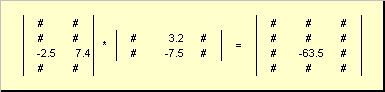
Fig.7 Element of the product of matrices

The product of matrices depends on the order, i.e. AB ≠ BA, at least for dimensional reasons. It is said to be non-commutative. However, the product of matrices is associative. It means that ABC = (AB)C = A(BC). Moreover, it is also distributive, i.e. A(B+C) = AB+AC. It's obvious that AO = O.

1.4. Square matrices

If the number of columns of a matrix is ​​equal to the number of its rows ( I = J=N), then such a matrix is ​​called square. In this section, we will consider only such matrices. Among these matrices, one can single out matrices with special properties.

Solitary matrix (denoted I and sometimes E) is a matrix in which all elements are equal to zero, except for the diagonal ones, which are equal to 1, i.e.

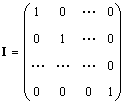
Obviously AI = IA = A.

The matrix is ​​called diagonal, if all its elements, except for the diagonal ones ( a ii) are equal to zero. for instance

Rice. 8 Diagonal matrix

Matrix A called the top triangular, if all its elements lying below the diagonal are equal to zero, i.e. a ij= 0, at i>j. for instance

Rice. 9 Upper triangular matrix

The lower triangular matrix is ​​defined similarly.

Matrix A called symmetrical, if A t = A. In other words a ij = a ji. for instance

Rice. 10 Symmetric matrix

Matrix A called orthogonal, if

A t A = AA t = I.

The matrix is ​​called normal if

1.5. Trace and determinant

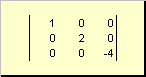
Following square matrix A(denoted Tr( A) or Sp( A)) is the sum of its diagonal elements,

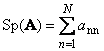
For instance,

Rice. 11 Matrix trace

It's obvious that

Sp(α A) = α Sp( A) and

Sp( A+B) = Sp( A)+ Sp( B).

It can be shown that

Sp( A) = Sp( A t), Sp( I) = N,

and also that

Sp( AB) = Sp( BA).

Another important characteristic of a square matrix is ​​its determinant(denoted by det( A)). The definition of the determinant in the general case is rather complicated, so we will start with the simplest option - the matrix A dimension (2×2). Then

For a (3×3) matrix, the determinant will be equal to

In the case of a matrix ( N× N) the determinant is calculated as the sum 1 2 3 ... N= N! terms, each of which is equal to

Indices k 1 , k 2 ,..., k N are defined as all possible ordered permutations r numbers in the set (1, 2, ... , N). The calculation of the matrix determinant is a complex procedure, which in practice is carried out using special programs. For instance,

Rice. 12 Matrix determinant

We note only the obvious properties:

det( I) = 1, det( A) = det( A t),

det( AB) = det( A)det( B).

1.6. Vectors

If the matrix has only one column ( J= 1), then such an object is called vector. More precisely, a column vector. for instance

Matrices consisting of one row can also be considered, for example

This object is also a vector, but row vector. When analyzing data, it is important to understand which vectors we are dealing with - columns or rows. So the spectrum taken for one sample can be considered as a row vector. Then the set of spectral intensities at some wavelength for all samples should be treated as a column vector.

The dimension of a vector is the number of its elements.

It is clear that any column vector can be transformed into a row vector by transposition, i.e.

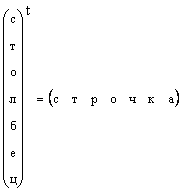
In those cases where the form of a vector is not specifically specified, but simply a vector is said, then they mean a column vector. We will also adhere to this rule. A vector is denoted by a lowercase direct bold letter. A zero vector is a vector all elements of which are equal to zero. It is denoted 0 .

1.7. The simplest operations with vectors

Vectors can be added and multiplied by numbers in the same way as matrices. For instance,

Rice. 13 Operations with vectors

Two vectors x and y called collinear, if there is a number α such that

1.8. Products of vectors

Two vectors of the same dimension N can be multiplied. Let there be two vectors x = (x 1 , x 2 ,...,x N) t and y = (y 1 , y 2 ,...,y N) t . Guided by the multiplication rule "row by column", we can make two products from them: x t y and xy t . First work

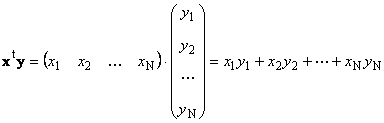
called scalar or internal. Its result is a number. It also uses the notation ( x,y)= x t y. For instance,

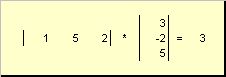
Rice. 14 Inner (scalar) product

Second work

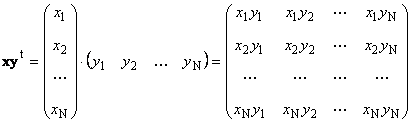
called external. Its result is a dimension matrix ( N× N). For instance,

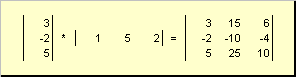
Rice. 15 Outer product

Vectors whose scalar product is equal to zero are called orthogonal.

1.9. Vector norm

The scalar product of a vector with itself is called a scalar square. This value

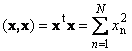
defines a square length vector x. To denote length (also called the norm vector) the notation is used

For instance,

Rice. 16 Vector norm

Unit length vector (|| x|| = 1) is called normalized. Nonzero vector ( x ≠ 0 ) can be normalized by dividing it by the length, i.e. x = ||x|| (x/||x||) = ||x|| e. Here e = x/||x|| is a normalized vector.

Vectors are called orthonormal if they are all normalized and pairwise orthogonal.

1.10. Angle between vectors

The scalar product defines and injectionφ between two vectors x and y

If the vectors are orthogonal, then cosφ = 0 and φ = π/2, and if they are collinear, then cosφ = 1 and φ = 0.

1.11. Vector representation of a matrix

Each matrix A size I× J can be represented as a set of vectors

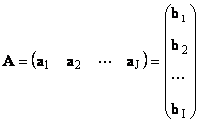
Here each vector a j is an j-th column and row vector b i is an i-th row of the matrix A

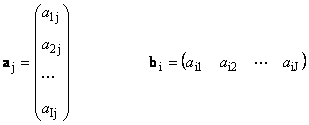
1.12. Linearly dependent vectors

Vectors of the same dimension ( N) can be added and multiplied by a number, just like matrices. The result is a vector of the same dimension. Let there be several vectors of the same dimension x 1 , x 2 ,...,x K and the same number of numbers α α 1 , α 2 ,...,α K. Vector

y= α 1 x 1 + α 2 x 2 +...+α K x K

called linear combination vectors x k .

If there are such non-zero numbers α k ≠ 0, k = 1,..., K, what y = 0 , then such a set of vectors x k called linearly dependent. Otherwise, the vectors are called linearly independent. For example, vectors x 1 = (2, 2) t and x 2 = (−1, −1) t are linearly dependent, since x 1 +2x 2 = 0

1.13. Matrix rank

Consider a set of K vectors x 1 , x 2 ,...,x K dimensions N. The rank of this system of vectors is the maximum number of linearly independent vectors. For example in the set

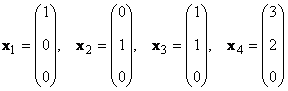
there are only two linearly independent vectors, for example x 1 and x 2 , so its rank is 2.

Obviously, if there are more vectors in the set than their dimension ( K>N), then they are necessarily linearly dependent.

Matrix rank(denoted by rank( A)) is the rank of the system of vectors it consists of. Although any matrix can be represented in two ways (column vectors or row vectors), this does not affect the rank value, since

1.14. inverse matrix

square matrix A is called non-degenerate if it has a unique reverse matrix A-1 , determined by the conditions

AA −1 = A −1 A = I.

The inverse matrix does not exist for all matrices. A necessary and sufficient condition for nondegeneracy is

det( A) ≠ 0 or rank( A) = N.

Matrix inversion is a complex procedure for which there are special programs. For instance,

Rice. 17 Matrix inversion

We give formulas for the simplest case - matrices 2 × 2

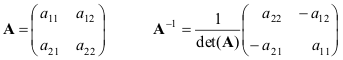
If matrices A and B are non-degenerate, then

(AB) −1 = B −1 A −1 .

1.15. Pseudo-inverse matrix

If the matrix A is degenerate and the inverse matrix does not exist, then in some cases one can use pseudo-inverse matrix, which is defined as such a matrix A+ that

AA + A = A.

The pseudo-inverse matrix is ​​not the only one and its form depends on the construction method. For example, for a rectangular matrix, you can use the Moore-Penrose method.

If the number of columns is less than the number of rows, then

A + =(A t A) −1 A t

For instance,

Rice. 17a Pseudo matrix inversion

If the number of columns more number lines, then

A + =A t( AA t) −1

1.16. Multiplication of a vector by a matrix

Vector x can be multiplied by a matrix A suitable dimension. In this case, the column vector is multiplied on the right Ax, and the vector string is on the left x t A. If the dimension of the vector J, and the dimension of the matrix I× J then the result is a vector of dimension I. For instance,

Rice. 18 Vector-Matrix Multiplication

If the matrix A- square ( I× I), then the vector y = Ax has the same dimension as x. It's obvious that

A(α 1 x 1 + α 2 x 2) = α 1 Ax 1 + α 2 Ax 2 .

Therefore matrices can be considered as linear transformations of vectors. In particular x = x, Ox = 0 .

2. Additional information

2.1. Systems of linear equations

Let A- matrix size I× J, a b- dimension vector J. Consider the equation

Ax = b

with respect to the vector x, dimensions I. Essentially, this is a system of I linear equations With J unknown x 1 ,...,x J. A solution exists if and only if

rank( A) = rank( B) = R,

where B is the augmented dimension matrix I×( J+1) consisting of the matrix A, padded with a column b, B = (A b). Otherwise, the equations are inconsistent.

If R = I = J, then the solution is unique

x = A −1 b.

If R < I, then there are many various solutions, which can be expressed in terms of a linear combination J−R vectors. System homogeneous equations Ax = 0 with a square matrix A (N× N) has a non-trivial solution ( x ≠ 0 ) if and only if det( A) = 0. If R= rank( A)<N, then there are N−R linearly independent solutions.

2.2. Bilinear and quadratic forms

If A is a square matrix, and x and y- vectors of the corresponding dimension, then the scalar product of the form x t Ay called bilinear the shape defined by the matrix A. At x = y expression x t Ax called quadratic form.

2.3. Positive definite matrices

square matrix A called positive definite, if for any nonzero vector x ≠ 0 ,

x t Ax > 0.

The negative (x t Ax < 0), non-negative (x t Ax≥ 0) and non-positive (x t Ax≤ 0) certain matrices.

2.4. Cholesky decomposition

If the symmetric matrix A is positive definite, then there is a unique triangular matrix U with positive elements, for which

A = U t U.

For instance,

Rice. 19 Cholesky decomposition

2.5. polar decomposition

Let A is a nondegenerate square matrix of dimension N× N. Then there is a unique polar representation

A = SR,

where S is a non-negative symmetric matrix, and R is an orthogonal matrix. matrices S and R can be defined explicitly:

S 2 = AA t or S = (AA t) ½ and R = S −1 A = (AA t) −½ A.

For instance,

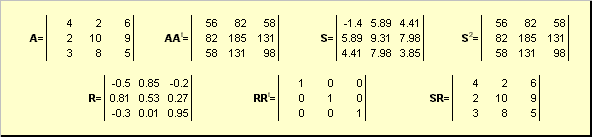
Rice. 20 Polar decomposition

If the matrix A is degenerate, then the decomposition is not unique - namely: S still alone, but R there may be many. Polar decomposition represents a matrix A as a compression/stretch combination S and turning R.

2.6. Eigenvectors and eigenvalues

Let A is a square matrix. Vector v called own vector matrices A, if

Av = λ v,

where the number λ is called eigenvalue matrices A. Thus, the transformation that the matrix performs A over vector v, is reduced to a simple stretching or compression with a factor λ. The eigenvector is determined up to multiplication by the constant α ≠ 0, i.e. if v is an eigenvector, then α v is also an eigenvector.

2.7. Eigenvalues

At the matrix A, dimension ( N× N) cannot be greater than N eigenvalues. They satisfy characteristic equation

det( A − λ I) = 0,

being algebraic equation N-th order. In particular, for a 2×2 matrix, the characteristic equation has the form

For instance,

Rice. 21 Eigenvalues

Set of eigenvalues ​​λ 1 ,..., λ N matrices A called spectrum A.

The spectrum has various properties. In particular

det( A) = λ 1×...×λ N, Sp( A) = λ 1 +...+λ N.

The eigenvalues ​​of an arbitrary matrix can be complex numbers, but if the matrix is ​​symmetric ( A t = A), then its eigenvalues are real.

2.8. Eigenvectors

At the matrix A, dimension ( N× N) cannot be greater than N eigenvectors, each of which corresponds to its own value. To determine the eigenvector v n you need to solve a system of homogeneous equations

(A − λ n I)v n = 0 .

It has a non-trivial solution because det( A-λ n I) = 0.

For instance,

Rice. 22 Eigenvectors

The eigenvectors of a symmetric matrix are orthogonal.

Eigenvalues ​​(numbers) and eigenvectors.
Solution examples

Be yourself

From both equations it follows that .

Let's put then: .

As a result: is the second eigenvector.

Let's repeat important points solutions:

– the resulting system certainly has common decision(the equations are linearly dependent);

- “Y” is selected in such a way that it is integer and the first “X” coordinate is integer, positive and as small as possible.

– we check that the particular solution satisfies each equation of the system.

Answer .

Intermediate "checkpoints" were quite enough, so the check of equalities, in principle, is superfluous.

V various sources information, the coordinates of eigenvectors are quite often written not in columns, but in rows, for example: (and, to be honest, I myself used to write them in lines). This option is acceptable, but in the light of the topic linear transformations technically more convenient to use column vectors.

Perhaps the solution seemed very long to you, but that's only because I commented on the first example in great detail.

Example 2

matrices

We train on our own! An approximate sample of the final design of the task at the end of the lesson.

Sometimes you need to do additional task, namely:

write the canonical decomposition of the matrix

What it is?

If the matrix eigenvectors form basis, then it can be represented as:

Where is a matrix composed of the coordinates of eigenvectors, – diagonal matrix with corresponding eigenvalues.

This matrix decomposition is called canonical or diagonal.

Consider the matrix of the first example. Her own vectors linearly independent(non-collinear) and form a basis. Let's make a matrix from their coordinates:

On the main diagonal matrices in due order eigenvalues ​​are located, and the remaining elements are equal to zero:
- once again I emphasize the importance of the order: "two" corresponds to the 1st vector and therefore is located in the 1st column, "three" - to the 2nd vector.

According to the usual algorithm for finding inverse matrix or Gauss-Jordan method find . No, that's not a typo! - in front of you is rare, like solar eclipse event when the inverse matched the original matrix.

It remains to write the canonical decomposition of the matrix :

The system can be solved with elementary transformations and in the following examples we will resort to this method. But here the “school” method works much faster. From the 3rd equation we express: - substitute into the second equation:

Since the first coordinate is zero, we obtain a system , from each equation of which it follows that .

And again pay attention to the mandatory presence of a linear relationship. If only a trivial solution is obtained , then either the eigenvalue was found incorrectly, or the system was compiled / solved with an error.

Compact coordinates gives value

Eigenvector:

And once again, we check that the found solution satisfies every equation of the system. In the following paragraphs and in subsequent tasks, I recommend that this wish be accepted as a mandatory rule.

2) For the eigenvalue, following the same principle, we obtain the following system:

From the 2nd equation of the system we express: - substitute into the third equation:

Since the "Z" coordinate is equal to zero, we obtain a system , from each equation of which a linear dependence follows.

Let

We check that the solution satisfies every equation of the system.

Thus, the eigenvector: .

3) And, finally, the system corresponds to its own value:

The second equation looks the simplest, so we express it from it and substitute it into the 1st and 3rd equations:

Everything is fine - a linear dependence was revealed, which we substitute into the expression:

As a result, "X" and "Y" were expressed through "Z": . In practice, it is not necessary to achieve just such relationships; in some cases it is more convenient to express both through or and through . Or even a “train” - for example, “X” through “Y”, and “Y” through “Z”

Let's put then:

We check that the found solution satisfies each equation of the system and write the third eigenvector

Answer: eigenvectors:

Geometrically, these vectors define three different spatial directions ("There and back again"), according to which linear transformation transforms nonzero vectors (eigenvectors) into vectors collinear to them.

If by condition it was required to find a canonical expansion of , then this is possible here, because different eigenvalues ​​correspond to different linearly independent eigenvectors. We make a matrix from their coordinates, the diagonal matrix from relevant eigenvalues ​​and find inverse matrix .

If, according to the condition, it is necessary to write linear transformation matrix in the basis of eigenvectors, then we give the answer in the form . There is a difference, and a significant difference! For this matrix is ​​the matrix "de".

A problem with simpler calculations for independent solution:

Example 5

Find eigenvectors of linear transformation given by matrix

When finding your own numbers, try not to bring the case to a polynomial of the 3rd degree. In addition, your system solutions may differ from my solutions - there is no unambiguity here; and the vectors you find may differ from the sample vectors up to proportionality to their respective coordinates. For example, and . It is more aesthetically pleasing to present the answer in the form of , but it's okay if you stop at the second option. However, there are reasonable limits to everything, the version does not look very good anymore.

An approximate final sample of the assignment at the end of the lesson.

How to solve the problem in case of multiple eigenvalues?

The general algorithm remains the same, but it has its own peculiarities, and it is advisable to keep some parts of the solution in a more rigorous academic style:

Example 6

Find eigenvalues ​​and eigenvectors

Solution

Of course, let's capitalize the fabulous first column:

And, after factoring the square trinomial:

As a result, eigenvalues ​​are obtained, two of which are multiples.

Let's find the eigenvectors:

1) We will deal with a lone soldier according to a “simplified” scheme:

From the last two equations, the equality is clearly visible, which, obviously, should be substituted into the 1st equation of the system:

There is no better combination:
Eigenvector:

2-3) Now we remove a couple of sentries. In this case, it may be either two or one eigenvector. Regardless of the multiplicity of the roots, we substitute the value in the determinant , which brings us the following homogeneous system of linear equations:

Eigenvectors are exactly the vectors
fundamental decision system

Actually, throughout the lesson, we were only engaged in finding the vectors of the fundamental system. Just for the time being, this term was not particularly required. By the way, those dexterous students who, in camouflage homogeneous equations, will be forced to smoke it now.

The only action was to remove extra lines. The result is a "one by three" matrix with a formal "step" in the middle.
– basic variable, – free variables. There are two free variables, so there are also two vectors of the fundamental system.

Let's express the basic variable in terms of free variables: . The zero factor in front of the “x” allows it to take on absolutely any values ​​(which is also clearly visible from the system of equations).

In the context of this problem, it is more convenient to write the general solution not in a row, but in a column:

The pair corresponds to an eigenvector:
The pair corresponds to an eigenvector:

Note : sophisticated readers can pick up these vectors orally - just by analyzing the system , but some knowledge is needed here: there are three variables, system matrix rank- unit means fundamental decision system consists of 3 – 1 = 2 vectors. However, the found vectors are perfectly visible even without this knowledge, purely on an intuitive level. In this case, the third vector will be written even “more beautifully”: . However, I warn you, in another example, there may not be a simple selection, which is why the reservation is intended for experienced people. Besides, why not take as the third vector, say, ? After all, its coordinates also satisfy each equation of the system, and the vectors are linearly independent. This option, in principle, is suitable, but "crooked", since the "other" vector is a linear combination of vectors of the fundamental system.

Answer: eigenvalues: , eigenvectors:

A similar example for a do-it-yourself solution:

Example 7

Find eigenvalues ​​and eigenvectors

An approximate sample of finishing at the end of the lesson.

It should be noted that both in the 6th and 7th examples, a triple of linearly independent eigenvectors is obtained, and therefore the original matrix can be represented in the canonical expansion . But such raspberries do not happen in all cases:

Example 8

Solution: compose and solve the characteristic equation:

We expand the determinant by the first column:

We carry out further simplifications according to the considered method, avoiding a polynomial of the 3rd degree:

are eigenvalues.

Let's find the eigenvectors:

1) There are no difficulties with the root:

Do not be surprised, in addition to the kit, variables are also in use - there is no difference here.

From the 3rd equation we express - we substitute into the 1st and 2nd equations:

From both equations follows:

Let then:

2-3) For multiple values, we get the system .

Let us write down the matrix of the system and, using elementary transformations, bring it to a stepped form:

With matrix A, if there is a number l such that AX = lX.

In this case, the number l is called eigenvalue operator (matrix A) corresponding to the vector X.

In other words, an eigenvector is a vector that, under the action of a linear operator, transforms into a collinear vector, i.e. just multiply by some number. In contrast, improper vectors are more difficult to transform.

We write the definition of the eigenvector as a system of equations:

Let's move all the terms to the left side:

The last system can be written in matrix form as follows:

(A - lE)X \u003d O

The resulting system always has a zero solution X = O. Such systems in which all free terms are equal to zero are called homogeneous. If the matrix of such a system is square and its determinant is not zero, then by Cramer's formulas we always get only decision- zero. It can be proved that the system has non-zero solutions if and only if the determinant of this matrix is ​​equal to zero, i.e.

|A - lE| = = 0

This equation with unknown l is called characteristic equation (characteristic polynomial) matrix A (linear operator).

It can be proved that the characteristic polynomial of a linear operator does not depend on the choice of basis.

For example, let's find the eigenvalues ​​and eigenvectors of the linear operator given by the matrix A = .

To do this, we compose the characteristic equation |А - lЕ| = \u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; eigenvalues ​​l 1 = (2 - 12)/2 = -5; l 2 \u003d (2 + 12) / 2 \u003d 7.

To find the eigenvectors, we solve two systems of equations

(A + 5E) X = O

(A - 7E) X = O

For the first of them, the expanded matrix will take the form

,

whence x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, i.e. X (1) \u003d (- (2/3) s; s).

For the second of them, the expanded matrix will take the form

,

whence x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, i.e. X (2) \u003d ((2/3) s 1; s 1).

Thus, the eigenvectors of this linear operator are all vectors of the form (-(2/3)c; c) with eigenvalue (-5) and all vectors of the form ((2/3)c 1 ; c 1) with eigenvalue 7 .

It can be proved that the matrix of the operator A in the basis consisting of its eigenvectors is diagonal and has the form:

,

where l i are the eigenvalues ​​of this matrix.

The converse is also true: if the matrix A in some basis is diagonal, then all vectors of this basis will be eigenvectors of this matrix.

It can also be proved that if a linear operator has n pairwise distinct eigenvalues, then the corresponding eigenvectors are linearly independent, and the matrix of this operator in the corresponding basis has a diagonal form.

Let's explain this with the previous example. Let us take arbitrary non-zero values ​​c and c 1 , but such that the vectors X (1) and X (2) are linearly independent, i.e. would form a basis. For example, let c \u003d c 1 \u003d 3, then X (1) \u003d (-2; 3), X (2) \u003d (2; 3).

Let us verify the linear independence of these vectors:

12 ≠ 0. In this new basis, the matrix A will take the form A * = .

To verify this, we use the formula A * = C -1 AC. Let's find C -1 first.

C -1 = ;

Quadratic forms

quadratic form f (x 1, x 2, x n) from n variables is called the sum, each term of which is either the square of one of the variables, or the product of two different variables, taken with a certain coefficient: f (x 1, x 2, x n) = (a ij = a ji).

The matrix A, composed of these coefficients, is called matrix quadratic form. It's always symmetrical matrix (i.e., a matrix symmetric about the main diagonal, a ij = a ji).

In matrix notation, the quadratic form has the form f(X) = X T AX, where

Indeed

For example, let's write the quadratic form in matrix form.

To do this, we find a matrix of a quadratic form. Its diagonal elements are equal to the coefficients at the squares of the variables, and the remaining elements are equal to half of the corresponding coefficients of the quadratic form. So

Let the matrix-column of variables X be obtained by a nondegenerate linear transformation of the matrix-column Y, i.e. X = CY, where C is a non-degenerate matrix of order n. Then the quadratic form f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Thus, under a non-degenerate linear transformation C, the matrix of the quadratic form takes the form: A * = C T AC.

For example, let's find the quadratic form f(y 1, y 2) obtained from the quadratic form f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 by a linear transformation.

The quadratic form is called canonical(It has canonical view) if all its coefficients a ij = 0 for i ≠ j, i.e.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.

Its matrix is ​​diagonal.

Theorem(the proof is not given here). Any quadratic form can be reduced to a canonical form using a non-degenerate linear transformation.

For example, let us reduce to the canonical form the quadratic form
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

To do this, first select the full square for the variable x 1:

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2) 2 - 5x 2 2 - x 2 x 3.

Now we select the full square for the variable x 2:

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

Then the non-degenerate linear transformation y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 and y 3 \u003d x 3 brings this quadratic form to the canonical form f (y 1, y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

Note that the canonical form of a quadratic form is defined ambiguously (the same quadratic form can be reduced to the canonical form different ways). However, the different ways canonical forms have a number common properties. In particular, the number of terms with positive (negative) coefficients of a quadratic form does not depend on how the form is reduced to this form (for example, in the considered example there will always be two negative and one positive coefficient). This property is called the law of inertia of quadratic forms.

Let us verify this by reducing the same quadratic form to the canonical form in a different way. Let's start the transformation with the variable x 2:

f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, where y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6) x 3 and y 3 = x 1 . Here negative coefficient-3 at y 1 and two positive coefficients 3 and 2 at y 2 and y 3 (and using another method, we got a negative coefficient (-5) at y 2 and two positive coefficients: 2 at y 1 and 1/20 at y 3 ).

It should also be noted that the rank of a matrix of a quadratic form, called the rank of the quadratic form, is equal to the number non-zero coefficients of the canonical form and does not change under linear transformations.

The quadratic form f(X) is called positively (negative) certain, if for all values ​​of the variables that are not simultaneously equal to zero, it is positive, i.e. f(X) > 0 (negative, i.e.
f(X)< 0).

For example, the quadratic form f 1 (X) \u003d x 1 2 + x 2 2 is positive definite, because is the sum of squares, and the quadratic form f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 is negative definite, because represents it can be represented as f 2 (X) \u003d - (x 1 - x 2) 2.

Most practical situations it is somewhat more difficult to establish the sign-definiteness of a quadratic form, so one of the following theorems is used for this (we formulate them without proofs).

Theorem. A quadratic form is positive (negative) definite if and only if all eigenvalues ​​of its matrix are positive (negative).

Theorem(Sylvester's criterion). A quadratic form is positive definite if and only if all principal minors of the matrix of this form are positive.

Major (corner) minor The k-th order of the matrix A of the n-th order is called the determinant of the matrix, composed of the first k rows and columns of the matrix A ().

Note that for negative-definite quadratic forms, the signs of the principal minors alternate, and the first-order minor must be negative.

For example, we examine the quadratic form f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 for sign-definiteness.

= (2 - l)*
*(3 - l) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D = 25 - 8 = 17;
. Therefore, the quadratic form is positive definite.

Method 2. The main minor of the first order of the matrix A D 1 = a 11 = 2 > 0. The main minor of the second order D 2 = = 6 - 4 = 2 > 0. Therefore, according to the Sylvester criterion, the quadratic form is positive definite.

We examine another quadratic form for sign-definiteness, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Method 1. Let's construct a matrix of quadratic form А = . The characteristic equation will have the form = (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
. Therefore, the quadratic form is negative definite.

Method 2. The main minor of the first order of the matrix A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Therefore, according to the Sylvester criterion, the quadratic form is negative definite (the signs of the principal minors alternate, starting from minus).

And as another example, we examine the quadratic form f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 for sign-definiteness.

Method 1. Let's construct a matrix of quadratic form А = . The characteristic equation will have the form = (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

One of these numbers is negative and the other is positive. The signs of the eigenvalues ​​are different. Therefore, a quadratic form cannot be either negative or positive definite, i.e. this quadratic form is not sign-definite (it can take values ​​of any sign).

Method 2. The main minor of the first order of the matrix A D 1 = a 11 = 2 > 0. The main minor of the second order D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

Diagonal-type matrices are most simply arranged. The question arises whether it is possible to find a basis in which the matrix of a linear operator would have a diagonal form. Such a basis exists.
Let a linear space R n and a linear operator A acting in it be given; in this case, the operator A takes R n into itself, that is, A:R n → R n .

Definition. A non-zero vector is called an eigenvector of the operator A if the operator A translates into a vector collinear to it, that is, . The number λ is called the eigenvalue or eigenvalue of the operator A corresponding to the eigenvector .
We note some properties of eigenvalues ​​and eigenvectors.
1. Any linear combination of eigenvectors of the operator A corresponding to the same eigenvalue λ is an eigenvector with the same eigenvalue.
2. Eigenvectors operator A with pairwise distinct eigenvalues ​​λ 1 , λ 2 , …, λ m are linearly independent.
3. If the eigenvalues ​​λ 1 =λ 2 = λ m = λ, then the eigenvalue λ corresponds to no more than m linearly independent eigenvectors.

So, if there are n linearly independent eigenvectors corresponding to different eigenvalues ​​λ 1 , λ 2 , …, λ n , then they are linearly independent, therefore, they can be taken as the basis of the space R n . Let us find the form of the matrix of the linear operator A in the basis of its eigenvectors, for which we act with the operator A on the basis vectors: then .
Thus, the matrix of the linear operator A in the basis of its eigenvectors has a diagonal form, and the eigenvalues ​​of the operator A are on the diagonal.
Is there another basis in which the matrix has a diagonal form? The answer to this question is given by the following theorem.

Theorem. The matrix of a linear operator A in the basis (i = 1..n) has a diagonal form if and only if all vectors of the basis are eigenvectors of the operator A.

Rule for finding eigenvalues ​​and eigenvectors

Let the vector , where x 1 , x 2 , …, x n - coordinates of the vector relative to the basis and is the eigenvector of the linear operator A corresponding to the eigenvalue λ , i.e. . This relation can be written in matrix form

. (*)

Equation (*) can be considered as an equation for finding , and , that is, we are interested in non-trivial solutions, since the eigenvector cannot be zero. It is known that nontrivial solutions of a homogeneous system of linear equations exist if and only if det(A - λE) = 0. Thus, for λ to be an eigenvalue of the operator A it is necessary and sufficient that det(A - λE) = 0.
If the equation (*) is written in detail in coordinate form, then we get a system of linear homogeneous equations:

(1)
where is the matrix of the linear operator.

System (1) has a nonzero solution if its determinant D is equal to zero

We got an equation for finding eigenvalues.
This equation is called the characteristic equation, and its left side is called the characteristic polynomial of the matrix (operator) A. If the characteristic polynomial has no real roots, then the matrix A has no eigenvectors and cannot be reduced to a diagonal form.
Let λ 1 , λ 2 , …, λ n be the real roots of the characteristic equation, and there may be multiples among them. Substituting these values ​​in turn into system (1), we find the eigenvectors.

Example 12. The linear operator A acts in R 3 according to the law , where x 1 , x 2 , .., x n are the coordinates of the vector in the basis , , . Find the eigenvalues ​​and eigenvectors of this operator.
Solution. We build the matrix of this operator:
.
We compose a system for determining the coordinates of eigenvectors:

We compose the characteristic equation and solve it:

.
λ 1,2 = -1, λ 3 = 3.
Substituting λ = -1 into the system, we have:
or
Because , then there are two dependent variables and one free variable.
Let x 1 be a free unknown, then We solve this system in any way and find the general solution of this system: Fundamental system solutions consists of one solution, since n - r = 3 - 2 = 1.
The set of eigenvectors corresponding to the eigenvalue λ = -1 has the form: , where x 1 is any number other than zero. Let's choose one vector from this set, for example, by setting x 1 = 1: .
Arguing similarly, we find the eigenvector corresponding to the eigenvalue λ = 3: .
In the space R 3 the basis consists of three linearly independent vectors, but we have obtained only two linearly independent eigenvectors, from which the basis in R 3 cannot be formed. Consequently, the matrix A of a linear operator cannot be reduced to a diagonal form.

Example 13 Given a matrix .
1. Prove that the vector is an eigenvector of the matrix A. Find the eigenvalue corresponding to this eigenvector.
2. Find a basis in which the matrix A has a diagonal form.
Solution.
1. If , then is an eigenvector

.
Vector (1, 8, -1) is an eigenvector. Eigenvalue λ = -1.
The matrix has a diagonal form in the basis consisting of eigenvectors. One of them is famous. Let's find the rest.
We are looking for eigenvectors from the system:

Characteristic equation: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Find the eigenvector corresponding to the eigenvalue λ = -3:

The rank of the matrix of this system is equal to two and is equal to the number of unknowns, therefore this system has only a zero solution x 1 = x 3 = 0. x 2 here can be anything other than zero, for example, x 2 = 1. Thus, the vector (0 ,1,0) is an eigenvector corresponding to λ = -3. Let's check:
.
If λ = 1, then we get the system
The rank of the matrix is ​​two. Cross out the last equation.
Let x 3 be the free unknown. Then x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
Assuming x 3 = 1, we have (-3,-9,1) - an eigenvector corresponding to the eigenvalue λ = 1. Check:

.
Since the eigenvalues ​​are real and different, the vectors corresponding to them are linearly independent, so they can be taken as a basis in R 3 . Thus, in the basis , , matrix A has the form:
.
Not every matrix of a linear operator A:R n → R n can be reduced to a diagonal form, since for some linear operators there may be less than n linearly independent eigenvectors. However, if the matrix is ​​symmetric, then exactly m linearly independent vectors correspond to the root of the characteristic equation of multiplicity m.

Definition. A symmetric matrix is ​​a square matrix in which the elements that are symmetric with respect to the main diagonal are equal, that is, in which .
Remarks. 1. All eigenvalues ​​of a symmetric matrix are real.
2. Eigenvectors of a symmetric matrix corresponding to pairwise different eigenvalues ​​are orthogonal.
As one of the numerous applications of the studied apparatus, we consider the problem of determining the form of a second-order curve.

Definition 9.3. Vector X called own vector matrices A if there is such a number λ, that the equality holds: A X= λ X, that is, the result of applying to X linear transformation given by the matrix A, is the multiplication of this vector by the number λ . The number itself λ called own number matrices A.

Substituting into formulas (9.3) x` j = λx j , we obtain a system of equations for determining the coordinates of the eigenvector:

. (9.5)

This linear homogeneous system will have a non-trivial solution only if its main determinant is 0 (Cramer's rule). By writing this condition in the form:

we get an equation for determining the eigenvalues λ called characteristic equation. Briefly, it can be represented as follows:

| A-λE | = 0, (9.6)

since its left side is the determinant of the matrix A-λE. Polynomial with respect to λ | A-λE| called characteristic polynomial matrices A.

Properties of the characteristic polynomial:

1) The characteristic polynomial of a linear transformation does not depend on the choice of the basis. Proof. (see (9.4)), but hence, . Thus, does not depend on the choice of basis. Hence, and | A-λE| does not change upon transition to a new basis.

2) If the matrix A linear transformation is symmetrical(those. a ij = a ji), then all the roots of the characteristic equation (9.6) are real numbers.

Properties of eigenvalues ​​and eigenvectors:

1) If we choose a basis from eigenvectors x 1, x 2, x 3 corresponding to the eigenvalues λ 1 , λ 2 , λ 3 matrices A, then in this basis the linear transformation A has a diagonal matrix:

(9.7) The proof of this property follows from the definition of eigenvectors.

2) If the transformation eigenvalues A are different, then the eigenvectors corresponding to them are linearly independent.

3) If the characteristic polynomial of the matrix A has three different roots, then in some basis the matrix A has a diagonal shape.

Let's find the eigenvalues ​​and eigenvectors of the matrix Let's make the characteristic equation: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Find the coordinates of the eigenvectors corresponding to each found value λ. From (9.5) it follows that if X (1) ={x 1 , x 2 , x 3) is the eigenvector corresponding to λ 1 = -2, then

is a collaborative but indeterminate system. Its solution can be written as X (1) ={a,0,-a), where a is any number. In particular, if you require that | x (1) |=1, X (1) =

Substituting into the system (9.5) λ 2 =3, we get a system for determining the coordinates of the second eigenvector - x (2) ={y1,y2,y3}:

, where X (2) ={b,-b,b) or, provided | x (2) |=1, x (2) =

For λ 3 = 6 find the eigenvector x (3) ={z1, z2, z3}:

, x (3) ={c,2c,c) or in the normalized version

x (3) = It can be seen that X (1) X (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = bc- 2bc + bc= 0. Thus, the eigenvectors of this matrix are pairwise orthogonal.

Lecture 10

Quadratic forms and their connection with symmetric matrices. Properties of eigenvectors and eigenvalues ​​of a symmetric matrix. Reduction of a quadratic form to a canonical form.

Definition 10.1.quadratic form real variables x 1, x 2,…, x n a polynomial of the second degree with respect to these variables is called, which does not contain a free term and terms of the first degree.

Examples of quadratic forms:

(n = 2),

(n = 3). (10.1)

Recall the definition of a symmetric matrix given in the last lecture:

Definition 10.2. The square matrix is ​​called symmetrical, if , that is, if the matrix elements symmetric with respect to the main diagonal are equal.

Properties of eigenvalues ​​and eigenvectors of a symmetric matrix:

1) All eigenvalues ​​of a symmetric matrix are real.

Proof (for n = 2).

Let the matrix A looks like: . Let's make the characteristic equation:

(10.2) Find the discriminant:

Therefore, the equation has only real roots.

2) The eigenvectors of a symmetric matrix are orthogonal.

Proof (for n= 2).

The coordinates of the eigenvectors and must satisfy the equations.