How to tackle the first wonderful limit. Wonderful limits

From the above article, you can find out what the limit is, and what it is eaten with - this is VERY important. Why? You may not understand what determinants are and successfully solve them, you may not understand at all what a derivative is and find them in the top five. But if you do not understand what the limit is, then it will be difficult to solve practical tasks. Also, it will not be superfluous to get acquainted with the samples of the design of solutions and my recommendations for design. All information is presented in a simple and accessible form.

And for the purposes of this lesson, we need the following teaching materials: Wonderful limits and Trigonometric formulas... They can be found on the page. It is best to print the manuals - it is much more convenient, and besides, they often have to be accessed offline.

Why are wonderful limits so wonderful? The remarkable thing about these limits is that they are proved greatest minds famous mathematicians, and grateful descendants do not have to suffer from terrible limits with a pile trigonometric functions, logarithms, degrees. That is, when finding the limits, we will use ready-made results that have been theoretically proven.

There are several remarkable limits, but in practice, part-time students in 95% of cases have two remarkable limits: First wonderful limit , Second wonderful limit... It should be noted that these are historically established names, and when, for example, they speak of “the first wonderful limit,” they mean by this a very definite thing, and not some random limit taken from the ceiling.

The first wonderful limit

Consider the following limit: (instead of the native letter "he" I will use the Greek letter "alpha", it is more convenient from the point of view of material presentation).

According to our rule of finding limits (see article Limits. Examples of solutions) we try to substitute zero into the function: in the numerator we get zero (the sine of zero is zero), in the denominator, obviously, is also zero. Thus, we are faced with an uncertainty of the species, which, fortunately, does not need to be disclosed. In the course of mathematical analysis, it is proved that:

This mathematical fact is called The first wonderful limit... I will not give an analytical proof of the limit, but we will consider its geometric meaning in the lesson about infinitesimal functions.

Often in practical assignments functions can be arranged differently, this does not change anything:

- the same first wonderful limit.

But you cannot rearrange the numerator and denominator on your own! If the limit is given in the form, then it must be solved in the same form, without rearranging anything.

In practice, not only a variable can act as a parameter, but also elementary function, complex function. It is only important that she strives for zero..

Examples:
, , ,

Here , , , and it's all good - the first wonderful limit is applicable.

But the next entry is heresy:

Why? Because the polynomial does not tend to zero, it tends to the five.

By the way, a question for filling, why equal to the limit ? The answer can be found at the end of the lesson.

In practice, not everything is so smooth, almost never a student will be offered to solve the free limit and get an easy test. Hmmm ... I am writing these lines, and a very important thought came to my mind - after all, "free" mathematical definitions and formulas seem to be better remembered by heart, this can provide invaluable help in the test, when the issue will be decided between "two" and "three", and the teacher decides to ask the student some simple question or suggest solving simplest example(“Maybe he (a) still knows what ?!”).

Let's move on to consideration practical examples:

Example 1

Find the limit

If we notice a sine in the limit, then this should immediately prompt us to think about the possibility of applying the first remarkable limit.

First, we try to substitute 0 in the expression under the limit sign (we do this mentally or on a draft):

So, we have an uncertainty of the kind, its be sure to indicate in the design of the solution. The expression under the limit sign looks like the first remarkable limit, but this is not exactly it, it is located under the sine, but in the denominator.

In such cases, we need to organize the first remarkable limit ourselves, using an artificial trick. The line of reasoning can be as follows: “under the sine we have, it means that we also need to get in the denominator”.
And this is done very simply:

That is, the denominator is artificially multiplied in this case by 7 and divided by the same seven. Now the recording has taken on a familiar shape.
When the task is drawn up by hand, it is advisable to mark the first remarkable limit with a simple pencil:

What happened? In fact, the circled expression has turned into a unit and disappeared in the work:

Now it only remains to get rid of the three-story fraction:

If you have forgotten the simplification of multilevel fractions, please refresh the material in the reference book. Hot Formulas School Mathematics Course .

Ready. Final answer:

If you don't want to use pencil marks, then the solution can be made as follows:

“

Using the first wonderful limit

“

Example 2

Find the limit

Again we see a fraction and a sine in the limit. We try to substitute zero in the numerator and denominator:

Indeed, we have uncertainty and, therefore, we must try to organize the first remarkable limit. At the lesson Limits. Examples of solutions we considered the rule that when we have uncertainty, then we need to factor out the numerator and denominator. Here - the same thing, we will represent the degrees in the form of a product (factors):

Similarly to the previous example, we outline the remarkable limits with a pencil (there are two of them here), and indicate that they tend to unity:

Actually, the answer is ready:

In the following examples, I will not be engaged in arts in Paint, I think how to correctly draw up a solution in a notebook - you already understand.

Example 3

Find the limit

Substitute zero in the expression under the limit sign:

Uncertainty has been received that needs to be disclosed. If there is a tangent in the limit, then almost always it is converted into sine and cosine according to the well-known trigonometric formula (by the way, they do about the same with the cotangent, see. methodological material Hot trigonometric formulas On the page Mathematical formulas, tables and reference materials).

In this case:

The cosine of zero is equal to one, and it is easy to get rid of it (do not forget to mark that it tends to one):

Thus, if in the limit the cosine is a MULTIPLIER, then, roughly speaking, it must be turned into a unit, which disappears in the product.

Here everything turned out easier, without any multiplication and division. The first remarkable limit also turns into one and disappears in the work:

As a result, infinity is obtained, it also happens.

Example 4

Find the limit

We try to substitute zero in the numerator and denominator:

The uncertainty is obtained (the cosine of zero, as we remember, is equal to one)

We use the trigonometric formula. Take note! For some reason, the limits with the use of this formula are very common.

We move the constant factors outside the limit icon:

Let's organize the first wonderful limit:

Here we have only one remarkable limit, which turns into a unit and disappears in the work:

Let's get rid of the three-story structure:

The limit is actually solved, we indicate that the remaining sine tends to zero:

Example 5

Find the limit

This example is more complicated, try to figure it out yourself:

Some limits can be reduced to the 1st wonderful limit by changing a variable, you can read about this a little later in the article Limit solving methods.

Second wonderful limit

In the theory of mathematical analysis, it is proved that:

This fact is called second wonderful limit.

Reference: Is an irrational number.

As a parameter, not only a variable can act, but also a complex function. It is only important that she strives for infinity..

Example 6

Find the limit

When the expression under the limit sign is in power, this is the first indication that a second remarkable limit should be attempted.

But first, as always, we try to substitute endlessly big number into an expression on what principle this is done, disassembled in the lesson Limits. Examples of solutions.

It is easy to see that for the base of the degree, and the exponent is , that is, there is an uncertainty of the form:

This uncertainty is just revealed with the help of the second remarkable limit. But, as often happens, the second remarkable limit does not lie on a silver platter, and must be artificially organized. You can argue as follows: in this example parameter, which means that we also need to organize in the indicator. To do this, we raise the base to a power, and so that the expression does not change, we raise it to a power:

When the task is completed by hand, we mark with a pencil:

Almost everything is ready, the terrible degree has turned into a pretty letter:

In this case, the limit icon itself is moved to the indicator:

Example 7

Find the limit

Attention! This type of limit is very common, please study this example very carefully.

We try to substitute an infinitely large number in the expression under the limit sign:

The result is uncertainty. But a second remarkable limit applies to species uncertainty. What to do? You need to convert the base of the degree. We argue this way: in our denominator, it means that in the numerator we also need to organize.

The formula for the second remarkable limit is lim x → ∞ 1 + 1 x x = e. Another notation looks like this: lim x → 0 (1 + x) 1 x = e.

When we talk about the second remarkable limit, we have to deal with an uncertainty of the form 1 ∞, i.e. a unit to an infinite degree.

Yandex.RTB R-A-339285-1

Consider problems in which the ability to calculate the second remarkable limit will come in handy.

Example 1

Find the limit lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4.

Solution

Substitute the desired shape lu and perform the calculations.

lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = 1 - 2 ∞ 2 + 1 ∞ 2 + 1 4 = 1 - 0 ∞ = 1 ∞

In our answer, we got one to the power of infinity. To determine the solution method, we use the table of uncertainties. Let's choose the second remarkable limit and make a change of variables.

t = - x 2 + 1 2 ⇔ x 2 + 1 4 = - t 2

If x → ∞, then t → - ∞.

Let's see what we got after the replacement:

lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = 1 ∞ = lim x → ∞ 1 + 1 t - 1 2 t = lim t → ∞ 1 + 1 t t - 1 2 = e - 1 2

Answer: lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = e - 1 2.

Example 2

Compute the limit lim x → ∞ x - 1 x + 1 x.

Solution

Substitute infinity and get the following.

lim x → ∞ x - 1 x + 1 x = lim x → ∞ 1 - 1 x 1 + 1 x x = 1 - 0 1 + 0 ∞ = 1 ∞

In the answer, we again got the same thing as in the previous problem, therefore, we can again use the second remarkable limit. Next, we need to select at the base power function whole part:

x - 1 x + 1 = x + 1 - 2 x + 1 = x + 1 x + 1 - 2 x + 1 = 1 - 2 x + 1

After that, the limit takes the following form:

lim x → ∞ x - 1 x + 1 x = 1 ∞ = lim x → ∞ 1 - 2 x + 1 x

We replace the variables. Suppose that t = - x + 1 2 ⇒ 2 t = - x - 1 ⇒ x = - 2 t - 1; if x → ∞, then t → ∞.

After that, we write down what we got in the original limit:

lim x → ∞ x - 1 x + 1 x = 1 ∞ = lim x → ∞ 1 - 2 x + 1 x = lim x → ∞ 1 + 1 t - 2 t - 1 = = lim x → ∞ 1 + 1 t - 2 t 1 + 1 t - 1 = lim x → ∞ 1 + 1 t - 2 t lim x → ∞ 1 + 1 t - 1 = = lim x → ∞ 1 + 1 tt - 2 1 + 1 ∞ = e - 2 (1 + 0) - 1 = e - 2

To perform this transformation, we used the basic properties of limits and degrees.

Answer: lim x → ∞ x - 1 x + 1 x = e - 2.

Example 3

Find the limit lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5.

Solution

lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = lim x → ∞ 1 + 1 x 3 1 + 2 x - 1 x 3 3 2 x - 5 x 4 = = 1 + 0 1 + 0 - 0 3 0 - 0 = 1 ∞

After that, we need to transform the function to apply the second remarkable limit. We got the following:

lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = 1 ∞ = lim x → ∞ x 3 - 2 x 2 - 1 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5

Since now we have the same exponents in the numerator and denominator of the fraction (equal to six), the limit of the fraction at infinity will be equal to the ratio of these coefficients at the highest powers.

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 6 2 = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 3

Replacing t = x 2 + 2 x 2 - 1 - 2 x 2 + 2 gives us a second remarkable limit. Means what:

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 3 = lim x → ∞ 1 + 1 tt - 3 = e - 3

Answer: lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = e - 3.

conclusions

Uncertainty 1 ∞, i.e. unit to an infinite degree is a power uncertainty, therefore, it can be expanded using the rules for finding the limits of exponential functions.

If you notice an error in the text, please select it and press Ctrl + Enter

The first remarkable limit is often used to calculate the limits containing sine, arcsine, tangent, arctangent and the resulting uncertainties of zero divided by zero.

Formula

The formula for the first remarkable limit is: $$ \ lim _ (\ alpha \ to 0) \ frac (\ sin \ alpha) (\ alpha) = 1 $$

We note that for $ \ alpha \ to 0 $ we get $ \ sin \ alpha \ to 0 $, thus, in the numerator and in the denominator we have zeros. Thus, the formula for the first remarkable limit is needed to disclose the uncertainties $ \ frac (0) (0) $.

To apply the formula, two conditions must be met:

The expressions in the sine and denominator of the fraction are the same
Expressions in the sine and denominator of a fraction tend to zero

Attention! $ \ lim_ (x \ to 0) \ frac (\ sin (2x ^ 2 + 1)) (2x ^ 2 + 1) \ neq 1 $ Although the expressions under the sine and in the denominator are the same, however, $ 2x ^ 2 + 1 = 1 $, for $ x \ to 0 $. The second condition is not met, therefore, the formula is NOT allowed!

Consequences

Rarely enough in the tasks you can see a clean first remarkable limit in which you could immediately write down the answer. In practice, things look a little more complicated, but in such cases it will be useful to know the consequences of the first remarkable limit. Thanks to them, you can quickly calculate the required limits.

$$ \ lim _ (\ alpha \ to 0) \ frac (\ alpha) (\ sin \ alpha) = 1 $$

$$ \ lim _ (\ alpha \ to 0) \ frac (\ sin (a \ alpha)) (\ sin (b \ alpha)) = \ frac (a) (b) $$

$$ \ lim _ (\ alpha \ to 0) \ frac (tg \ alpha) (\ alpha) = 1 $$

$$ \ lim _ (\ alpha \ to 0) \ frac (\ arcsin \ alpha) (\ alpha) = 1 $$

$$ \ lim _ (\ alpha \ to 0) \ frac (arctg \ alpha) (\ alpha) = 1 $$

Examples of solutions

Consider the first remarkable limit, examples of the solution of which on the calculation of limits containing trigonometric functions and uncertainty $ \ bigg [\ frac (0) (0) \ bigg] $

Example 1
Evaluate $ \ lim_ (x \ to 0) \ frac (\ sin2x) (4x) $
Solution
Consider the limit and note that there is a sine in it. Next, substitute $ x = 0 $ in the numerator and denominator and get the uncertainty zero divided by zero: $$ \ lim_ (x \ to 0) \ frac (\ sin2x) (4x) = \ frac (0) (0) $$ Already two signs that you need to apply a wonderful limit, but there is a small nuance: we cannot immediately apply the formula, since the expression under the sine sign differs from the expression in the denominator. And we need them to be equal. Therefore, using elementary transformations the numerator we will turn it into $ 2x $. To do this, we take two out of the denominator of the fraction by a separate factor. It looks like this: $$ \ lim_ (x \ to 0) \ frac (\ sin2x) (4x) = \ lim_ (x \ to 0) \ frac (\ sin2x) (2 \ cdot 2x) = $$ $$ = \ frac (1) (2) \ lim_ (x \ to 0) \ frac (\ sin2x) (2x) = \ frac (1) (2) \ cdot 1 = \ frac (1) (2) $$ Note that at the end $ \ lim_ (x \ to 0) \ frac (\ sin2x) (2x) = 1 $ is obtained by the formula. If you can't solve your problem, then send it to us. We will provide detailed solution... You will be able to familiarize yourself with the course of the calculation and get information. This will help you get credit from your teacher in a timely manner!
Answer
$$ \ lim_ (x \ to 0) \ frac (\ sin2x) (4x) = \ frac (1) (2) $$

Example 2
Find $ \ lim_ (x \ to 0) \ frac (\ sin (x ^ 3 + 2x)) (2x-x ^ 4) $
Solution
As always, you first need to know the type of uncertainty. If it is divided by zero, then we pay attention to the presence of a sine: $$ \ lim_ (x \ to 0) \ frac (\ sin (x ^ 3 + 2x)) (2x-x ^ 4) = \ frac (0) (0) = $$ This uncertainty allows us to use the formula for the first remarkable limit, but the expression from the denominator is not equal to the sine argument? Therefore, it is impossible to apply the formula "on the forehead". You need to multiply and divide the fraction by the sine argument: $$ = \ lim_ (x \ to 0) \ frac ((x ^ 3 + 2x) \ sin (x ^ 3 + 2x)) ((2x-x ^ 4) (x ^ 3 + 2x)) = $$ Now, by the properties of the limits, we write: $$ = \ lim_ (x \ to 0) \ frac ((x ^ 3 + 2x)) (2x-x ^ 4) \ cdot \ lim_ (x \ to 0) \ frac (\ sin (x ^ 3 + 2x)) ((x ^ 3 + 2x)) = $$ The second limit just fits the formula and is equal to one: $$ = \ lim_ (x \ to 0 ) \ frac (x ^ 3 + 2x) (2x-x ^ 4) \ cdot 1 = \ lim_ (x \ to 0) \ frac (x ^ 3 + 2x) (2x-x ^ 4) = $$ Substitute again $ x = 0 $ into a fraction and we get the uncertainty $ \ frac (0) (0) $. To eliminate it, it is sufficient to exclude $ x $ from brackets and reduce to it: $$ = \ lim_ (x \ to 0) \ frac (x (x ^ 2 + 2)) (x (2-x ^ 3)) = \ lim_ (x \ to 0) \ frac (x ^ 2 + 2) (2-x ^ 3) = $$ $$ = \ frac (0 ^ 2 + 2) (2 - 0 ^ 3) = \ frac (2 ) (2) = 1 $$
Answer
$$ \ lim_ (x \ to 0) \ frac (\ sin (x ^ 3 + 2x)) (2x-x ^ 4) = 1 $$

Example 4
Evaluate $ \ lim_ (x \ to0) \ frac (\ sin2x) (tg3x) $
Solution
Let's start the calculation by substituting $ x = 0 $. As a result, we get the uncertainty $ \ frac (0) (0) $. The limit contains sine and tangent, which hints at a possible development of the situation using the formula for the first remarkable limit. We transform the numerator and denominator of the fraction under the formula and consequence: $$ \ lim_ (x \ to0) \ frac (\ sin2x) (tg3x) = \ frac (0) (0) = \ lim_ (x \ to0) \ frac (\ frac (\ sin2x) (2x) \ cdot 2x ) (\ frac (tg3x) (3x) \ cdot 3x) = $$ Now we see expressions suitable for the formula and consequences appeared in the numerator and denominator. The sine argument and tangent argument are the same for the corresponding denominators $$ = \ lim_ (x \ to0) \ frac (1 \ cdot 2x) (1 \ cdot 3x) = \ frac (2) (3) $$
Answer
$$ \ lim_ (x \ to0) \ frac (\ sin2x) (tg2x) = \ frac (2) (3) $$

In the article: "The first remarkable limit, examples of solutions" was told about the cases in which it is advisable to use this formula and its consequences.

There are several wonderful limits, but the most famous are the first and second wonderful limits. The remarkable thing about these limits is that they are widely used and with their help you can find other limits that are found in numerous problems. This is what we will do in the practical part of this lesson. To solve problems by reducing them to the first or second remarkable limit, it is not necessary to disclose the uncertainties contained in them, since the values of these limits have long been deduced by great mathematicians.

The first wonderful limit is the limit of the ratio of the sine of an infinitesimal arc to the same arc, expressed in radian measure:

Let's move on to solving problems at the first remarkable limit. Note: if a trigonometric function is under the limit sign, this is almost a sure sign that this expression can be reduced to the first remarkable limit.

Example 1. Find the limit.

Solution. Substitution instead of x zero leads to uncertainty:

The denominator is sine, therefore, the expression can be reduced to the first remarkable limit. Let's start transformations:

The denominator contains the sine of three x, and the numerator has only one x, which means that you need to get three x in the numerator as well. For what? To represent 3 x = a and get an expression.

And we arrive at a variation on the first wonderful limit:

because it doesn't matter which letter (variable) is in this formula instead of the x.

We multiply x by three and then divide:

In accordance with the observed first remarkable limit, we replace the fractional expression:

Now we can finally solve this limit:

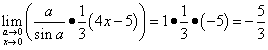Example 2. Find the limit.

Solution. Direct substitution again leads to the zero-divide-by-zero ambiguity:

To get the first remarkable limit, you need the x under the sine sign in the numerator and just the x in the denominator with the same coefficient. Let this coefficient be equal to 2. To do this, we represent the current coefficient at x as below, performing actions with fractions, we get:

Example 3. Find the limit.

Solution. When substituting, we again obtain the "zero divided by zero" uncertainty:

You probably already understand that from the original expression you can get the first wonderful limit multiplied by the first wonderful limit. To do this, we decompose the x squares in the numerator and the sine in the denominator by the same factors, and to get the same coefficients for the x and sine, divide the x in the numerator by 3 and then multiply by 3. We get:

Example 4. Find the limit.

Solution. Again we get the uncertainty "zero divided by zero":

We can get the ratio of the first two remarkable limits. Divide both the numerator and the denominator by x. Then, so that the coefficients for sines and for x coincide, we multiply the upper x by 2 and immediately divide by 2, and multiply the lower x by 3 and immediately divide by 3. We get:

Example 5. Find the limit.

Solution. And again the uncertainty "zero divided by zero":

Remember from trigonometry that the tangent is the ratio of the sine to the cosine, and the cosine of zero is equal to one. We make transformations and get:

Example 6. Find the limit.

Solution. The trigonometric function under the limit sign again suggests the idea of using the first remarkable limit. We represent it as the ratio of sine to cosine.

The first remarkable limit is called the following equality:

\ begin (equation) \ lim _ (\ alpha \ to (0)) \ frac (\ sin \ alpha) (\ alpha) = 1 \ end (equation)

Since for $ \ alpha \ to (0) $ we have $ \ sin \ alpha \ to (0) $, it is said that the first remarkable limit reveals an uncertainty of the form $ \ frac (0) (0) $. Generally speaking, in formula (1), instead of the variable $ \ alpha $ under the sine sign and in the denominator, any expression can be located, as long as two conditions are satisfied:

Expressions under the sine sign and in the denominator simultaneously tend to zero, i.e. there is an uncertainty of the form $ \ frac (0) (0) $.
The expressions under the sine sign and in the denominator are the same.

Consequences from the first remarkable limit are also often used:

\ begin (equation) \ lim _ (\ alpha \ to (0)) \ frac (\ tg \ alpha) (\ alpha) = 1 \ end (equation) \ begin (equation) \ lim _ (\ alpha \ to (0) ) \ frac (\ arcsin \ alpha) (\ alpha) = 1 \ end (equation) \ begin (equation) \ lim _ (\ alpha \ to (0)) \ frac (\ arctg \ alpha) (\ alpha) = 1 \ end (equation)

Eleven examples have been solved on this page. Example No. 1 is devoted to the proof of formulas (2) - (4). Examples # 2, # 3, # 4 and # 5 contain solutions with detailed comments. Examples 6-10 contain solutions with practically no comments, because detailed explanations were given in the previous examples. The solution uses some of the trigonometric formulas that can be found.

Note that the presence of trigonometric functions, coupled with the uncertainty $ \ frac (0) (0) $, does not mean that the first remarkable limit must be applied. Sometimes simple trigonometric transformations are enough - for example, see.

Example # 1

Prove that $ \ lim _ (\ alpha \ to (0)) \ frac (\ tg \ alpha) (\ alpha) = 1 $, $ \ lim _ (\ alpha \ to (0)) \ frac (\ arcsin \ alpha ) (\ alpha) = 1 $, $ \ lim _ (\ alpha \ to (0)) \ frac (\ arctg \ alpha) (\ alpha) = 1 $.

a) Since $ \ tg \ alpha = \ frac (\ sin \ alpha) (\ cos \ alpha) $, then:

$$ \ lim _ (\ alpha \ to (0)) \ frac (\ tg (\ alpha)) (\ alpha) = \ left | \ frac (0) (0) \ right | = \ lim _ (\ alpha \ to (0)) \ frac (\ sin (\ alpha)) (\ alpha \ cos (\ alpha)) $$

Since $ \ lim _ (\ alpha \ to (0)) \ cos (0) = 1 $ and $ \ lim _ (\ alpha \ to (0)) \ frac (\ sin \ alpha) (\ alpha) = 1 $ , then:

$$ \ lim _ (\ alpha \ to (0)) \ frac (\ sin (\ alpha)) (\ alpha \ cos (\ alpha)) = \ frac (\ displaystyle \ lim _ (\ alpha \ to (0)) \ frac (\ sin (\ alpha)) (\ alpha)) (\ displaystyle \ lim _ (\ alpha \ to (0)) \ cos (\ alpha)) = \ frac (1) (1) = 1. $$

b) Let's make the substitution $ \ alpha = \ sin (y) $. Since $ \ sin (0) = 0 $, then from the condition $ \ alpha \ to (0) $ we have $ y \ to (0) $. In addition, there is a neighborhood of zero in which $ \ arcsin \ alpha = \ arcsin (\ sin (y)) = y $, so:

$$ \ lim _ (\ alpha \ to (0)) \ frac (\ arcsin \ alpha) (\ alpha) = \ left | \ frac (0) (0) \ right | = \ lim_ (y \ to (0)) \ frac (y) (\ sin (y)) = \ lim_ (y \ to (0)) \ frac (1) (\ frac (\ sin (y)) ( y)) = \ frac (1) (\ displaystyle \ lim_ (y \ to (0)) \ frac (\ sin (y)) (y)) = \ frac (1) (1) = 1. $$

The equality $ \ lim _ (\ alpha \ to (0)) \ frac (\ arcsin \ alpha) (\ alpha) = 1 $ is proved.

c) Let's make the substitution $ \ alpha = \ tg (y) $. Since $ \ tg (0) = 0 $, the conditions $ \ alpha \ to (0) $ and $ y \ to (0) $ are equivalent. In addition, there is a neighborhood of zero in which $ \ arctg \ alpha = \ arctg \ tg (y)) = y $, therefore, based on the results of item a), we will have:

$$ \ lim _ (\ alpha \ to (0)) \ frac (\ arctg \ alpha) (\ alpha) = \ left | \ frac (0) (0) \ right | = \ lim_ (y \ to (0)) \ frac (y) (\ tg (y)) = \ lim_ (y \ to (0)) \ frac (1) (\ frac (\ tg (y)) ( y)) = \ frac (1) (\ displaystyle \ lim_ (y \ to (0)) \ frac (\ tg (y)) (y)) = \ frac (1) (1) = 1. $$

The equality $ \ lim _ (\ alpha \ to (0)) \ frac (\ arctg \ alpha) (\ alpha) = 1 $ is proved.

Equalities a), b), c) are often used along with the first remarkable limit.

Example No. 2

Compute limit of $ \ lim_ (x \ to (2)) \ frac (\ sin \ left (\ frac (x ^ 2-4) (x + 7) \ right)) (\ frac (x ^ 2-4) ( x + 7)) $.

Since $ \ lim_ (x \ to (2)) \ frac (x ^ 2-4) (x + 7) = \ frac (2 ^ 2-4) (2 + 7) = 0 $ and $ \ lim_ ( x \ to (2)) \ sin \ left (\ frac (x ^ 2-4) (x + 7) \ right) = \ sin (0) = 0 $, i.e. both the numerator and denominator of the fraction simultaneously tend to zero, then here we are dealing with an uncertainty of the form $ \ frac (0) (0) $, i.e. done. In addition, it can be seen that the expressions under the sine sign and in the denominator coincide (i.e., and are satisfied):

So, both conditions listed at the beginning of the page are met. From this it follows that the formula is applicable, i.e. $ \ lim_ (x \ to (2)) \ frac (\ sin \ left (\ frac (x ^ 2-4) (x + 7) \ right)) (\ frac (x ^ 2-4) (x + 7)) = 1 $.

Answer: $ \ lim_ (x \ to (2)) \ frac (\ sin \ left (\ frac (x ^ 2-4) (x + 7) \ right)) (\ frac (x ^ 2-4) (x +7)) = 1 $.

Example No. 3

Find $ \ lim_ (x \ to (0)) \ frac (\ sin (9x)) (x) $.

Since $ \ lim_ (x \ to (0)) \ sin (9x) = 0 $ and $ \ lim_ (x \ to (0)) x = 0 $, we are dealing with an uncertainty of the form $ \ frac (0 ) (0) $, i.e. done. However, the expressions under the sine sign and in the denominator do not match. Here you need to fit the expression in the denominator to the desired shape. We need the expression $ 9x $ in the denominator - then it will become true. In fact, we are missing the $ 9 multiplier in the denominator, which is not so difficult to introduce - just multiply the denominator expression by $ 9. Naturally, to compensate for the multiplication by $ 9, you will have to immediately by $ 9 and divide:

$$ \ lim_ (x \ to (0)) \ frac (\ sin (9x)) (x) = \ left | \ frac (0) (0) \ right | = \ lim_ (x \ to (0)) \ frac (\ sin (9x)) (9x \ cdot \ frac (1) (9)) = 9 \ lim_ (x \ to (0)) \ frac (\ sin (9x)) (9x) $$

Now the expressions in the denominator and under the sine sign coincide. Both conditions for the limit $ \ lim_ (x \ to (0)) \ frac (\ sin (9x)) (9x) $ are satisfied. Therefore, $ \ lim_ (x \ to (0)) \ frac (\ sin (9x)) (9x) = 1 $. This means that:

$$ 9 \ lim_ (x \ to (0)) \ frac (\ sin (9x)) (9x) = 9 \ cdot (1) = 9. $$

Answer: $ \ lim_ (x \ to (0)) \ frac (\ sin (9x)) (x) = 9 $.

Example No. 4

Find $ \ lim_ (x \ to (0)) \ frac (\ sin (5x)) (\ tg (8x)) $.

Since $ \ lim_ (x \ to (0)) \ sin (5x) = 0 $ and $ \ lim_ (x \ to (0)) \ tg (8x) = 0 $, here we are dealing with an uncertainty of the form $ \ frac (0) (0) $. However, the shape of the first remarkable limit is violated. A numerator containing $ \ sin (5x) $ requires $ 5x $ in the denominator. In this situation, the easiest way is to divide the numerator by $ 5x $, and then multiply by $ 5x $. In addition, we will perform a similar operation with the denominator, multiplying and dividing $ \ tg (8x) $ by $ 8x $:

$$ \ lim_ (x \ to (0)) \ frac (\ sin (5x)) (\ tg (8x)) = \ left | \ frac (0) (0) \ right | = \ lim_ (x \ to (0)) \ frac (\ frac (\ sin (5x)) (5x) \ cdot (5x)) (\ frac (\ tg (8x)) (8x) \ cdot (8x) ) $$

Reducing by $ x $ and moving the constant $ \ frac (5) (8) $ outside the limit sign, we get:

$$ \ lim_ (x \ to (0)) \ frac (\ frac (\ sin (5x)) (5x) \ cdot (5x)) (\ frac (\ tg (8x)) (8x) \ cdot (8x )) = \ frac (5) (8) \ cdot \ lim_ (x \ to (0)) \ frac (\ frac (\ sin (5x)) (5x)) (\ frac (\ tg (8x)) ( 8x)) $$

Note that $ \ lim_ (x \ to (0)) \ frac (\ sin (5x)) (5x) $ fully meets the requirements for the first remarkable limit. To find $ \ lim_ (x \ to (0)) \ frac (\ tg (8x)) (8x) $ the formula is applicable:

$$ \ frac (5) (8) \ cdot \ lim_ (x \ to (0)) \ frac (\ frac (\ sin (5x)) (5x)) (\ frac (\ tg (8x)) (8x )) = \ frac (5) (8) \ cdot \ frac (\ displaystyle \ lim_ (x \ to (0)) \ frac (\ sin (5x)) (5x)) (\ displaystyle \ lim_ (x \ to (0)) \ frac (\ tg (8x)) (8x)) = \ frac (5) (8) \ cdot \ frac (1) (1) = \ frac (5) (8). $$

Answer: $ \ lim_ (x \ to (0)) \ frac (\ sin (5x)) (\ tg (8x)) = \ frac (5) (8) $.

Example No. 5

Find $ \ lim_ (x \ to (0)) \ frac (\ cos (5x) - \ cos ^ 3 (5x)) (x ^ 2) $.

Since $ \ lim_ (x \ to (0)) (\ cos (5x) - \ cos ^ 3 (5x)) = 1-1 = 0 $ (remember that $ \ cos (0) = 1 $) and $ \ lim_ (x \ to (0)) x ^ 2 = 0 $, then we are dealing with an uncertainty of the form $ \ frac (0) (0) $. However, to apply the first remarkable limit, you need to get rid of the cosine in the numerator by moving to sines (in order to apply the formula later) or tangents (in order to apply the formula later). This can be done with the following transformation:

$$ \ cos (5x) - \ cos ^ 3 (5x) = \ cos (5x) \ cdot \ left (1- \ cos ^ 2 (5x) \ right) $$ $$ \ cos (5x) - \ cos ^ 3 (5x) = \ cos (5x) \ cdot \ left (1- \ cos ^ 2 (5x) \ right) = \ cos (5x) \ cdot \ sin ^ 2 (5x). $$

Let's go back to the limit:

$$ \ lim_ (x \ to (0)) \ frac (\ cos (5x) - \ cos ^ 3 (5x)) (x ^ 2) = \ left | \ frac (0) (0) \ right | = \ lim_ (x \ to (0)) \ frac (\ cos (5x) \ cdot \ sin ^ 2 (5x)) (x ^ 2) = \ lim_ (x \ to (0)) \ left (\ cos (5x) \ cdot \ frac (\ sin ^ 2 (5x)) (x ^ 2) \ right) $$

The fraction $ \ frac (\ sin ^ 2 (5x)) (x ^ 2) $ is already close to the form required for the first remarkable limit. Let's work a little with the fraction $ \ frac (\ sin ^ 2 (5x)) (x ^ 2) $, adjusting it to the first remarkable limit (note that the expressions in the numerator and under the sine must match):

$$ \ frac (\ sin ^ 2 (5x)) (x ^ 2) = \ frac (\ sin ^ 2 (5x)) (25x ^ 2 \ cdot \ frac (1) (25)) = 25 \ cdot \ frac (\ sin ^ 2 (5x)) (25x ^ 2) = 25 \ cdot \ left (\ frac (\ sin (5x)) (5x) \ right) ^ 2 $$

Let's return to the considered limit:

$$ \ lim_ (x \ to (0)) \ left (\ cos (5x) \ cdot \ frac (\ sin ^ 2 (5x)) (x ^ 2) \ right) = \ lim_ (x \ to (0 )) \ left (25 \ cos (5x) \ cdot \ left (\ frac (\ sin (5x)) (5x) \ right) ^ 2 \ right) = \\ = 25 \ cdot \ lim_ (x \ to ( 0)) \ cos (5x) \ cdot \ lim_ (x \ to (0)) \ left (\ frac (\ sin (5x)) (5x) \ right) ^ 2 = 25 \ cdot (1) \ cdot ( 1 ^ 2) = 25. $$

Answer: $ \ lim_ (x \ to (0)) \ frac (\ cos (5x) - \ cos ^ 3 (5x)) (x ^ 2) = 25 $.

Example No. 6

Find the limit $ \ lim_ (x \ to (0)) \ frac (1- \ cos (6x)) (1- \ cos (2x)) $.

Since $ \ lim_ (x \ to (0)) (1- \ cos (6x)) = 0 $ and $ \ lim_ (x \ to (0)) (1- \ cos (2x)) = 0 $, then we are dealing with the uncertainty $ \ frac (0) (0) $. Let's open it up with the first remarkable limit. To do this, let's move from cosines to sines. Since $ 1- \ cos (2 \ alpha) = 2 \ sin ^ 2 (\ alpha) $, then:

$$ 1- \ cos (6x) = 2 \ sin ^ 2 (3x); \; 1- \ cos (2x) = 2 \ sin ^ 2 (x). $$

Passing in the given limit to the sines, we will have:

$$ \ lim_ (x \ to (0)) \ frac (1- \ cos (6x)) (1- \ cos (2x)) = \ left | \ frac (0) (0) \ right | = \ lim_ (x \ to (0)) \ frac (2 \ sin ^ 2 (3x)) (2 \ sin ^ 2 (x)) = \ lim_ (x \ to (0)) \ frac (\ sin ^ 2 (3x)) (\ sin ^ 2 (x)) = \\ = \ lim_ (x \ to (0)) \ frac (\ frac (\ sin ^ 2 (3x)) ((3x) ^ 2) \ cdot (3x) ^ 2) (\ frac (\ sin ^ 2 (x)) (x ^ 2) \ cdot (x ^ 2)) = \ lim_ (x \ to (0)) \ frac (\ left (\ frac (\ sin (3x)) (3x) \ right) ^ 2 \ cdot (9x ^ 2)) (\ left (\ frac (\ sin (x)) (x) \ right) ^ 2 \ cdot (x ^ 2)) = 9 \ cdot \ frac (\ displaystyle \ lim_ (x \ to (0)) \ left (\ frac (\ sin (3x)) (3x) \ right) ^ 2) (\ displaystyle \ lim_ (x \ to (0)) \ left (\ frac (\ sin (x)) (x) \ right) ^ 2) = 9 \ cdot \ frac (1 ^ 2) (1 ^ 2) = 9. $$

Answer: $ \ lim_ (x \ to (0)) \ frac (1- \ cos (6x)) (1- \ cos (2x)) = 9 $.

Example No. 7

Compute the limit of $ \ lim_ (x \ to (0)) \ frac (\ cos (\ alpha (x)) - \ cos (\ beta (x))) (x ^ 2) $ assuming $ \ alpha \ neq \ beta $.

Detailed explanations were given earlier, but here we just note that there is again the uncertainty $ \ frac (0) (0) $. Let's go from cosines to sines using the formula

$$ \ cos \ alpha- \ cos \ beta = -2 \ sin \ frac (\ alpha + \ beta) (2) \ cdot \ sin \ frac (\ alpha- \ beta) (2). $$

Using the above formula, we get:

$$ \ lim_ (x \ to (0)) \ frac (\ cos (\ alpha (x)) - \ cos (\ beta (x))) (x ^ 2) = \ left | \ frac (0) ( 0) \ right | = \ lim_ (x \ to (0)) \ frac (-2 \ sin \ frac (\ alpha (x) + \ beta (x)) (2) \ cdot \ sin \ frac (\ alpha (x) - \ beta (x)) (2)) (x ^ 2) = \\ = -2 \ cdot \ lim_ (x \ to (0)) \ frac (\ sin \ left (x \ cdot \ frac (\ alpha + \ beta ) (2) \ right) \ cdot \ sin \ left (x \ cdot \ frac (\ alpha- \ beta) (2) \ right)) (x ^ 2) = -2 \ cdot \ lim_ (x \ to ( 0)) \ left (\ frac (\ sin \ left (x \ cdot \ frac (\ alpha + \ beta) (2) \ right)) (x) \ cdot \ frac (\ sin \ left (x \ cdot \ frac (\ alpha- \ beta) (2) \ right)) (x) \ right) = \\ = -2 \ cdot \ lim_ (x \ to (0)) \ left (\ frac (\ sin \ left (x \ cdot \ frac (\ alpha + \ beta) (2) \ right)) (x \ cdot \ frac (\ alpha + \ beta) (2)) \ cdot \ frac (\ alpha + \ beta) (2) \ cdot \ frac (\ sin \ left (x \ cdot \ frac (\ alpha- \ beta) (2) \ right)) (x \ cdot \ frac (\ alpha- \ beta) (2)) \ cdot \ frac (\ alpha- \ beta) (2) \ right) = \\ = - \ frac ((\ alpha + \ beta) \ cdot (\ alpha- \ beta)) (2) \ lim_ (x \ to (0)) \ frac (\ sin \ left (x \ cdot \ frac (\ alpha + \ beta) (2) \ right)) (x \ cdot \ frac (\ alpha + \ beta) (2)) \ cdot \ lim_ (x \ to (0)) \ frac (\ sin \ left (x \ cdot \ frac (\ alpha- \ beta) (2) \ right)) (x \ cdot \ frac (\ alpha- \ beta) (2)) = - \ frac (\ alpha ^ 2- \ beta ^ 2) (2) \ cdot (1) \ cdot (1) = \ frac (\ beta ^ 2- \ alpha ^ 2) (2). $$

Answer: $ \ lim_ (x \ to (0)) \ frac (\ cos (\ alpha (x)) - \ cos (\ beta (x))) (x ^ 2) = \ frac (\ beta ^ 2- \ alpha ^ 2) (2) $.

Example No. 8

Find the limit $ \ lim_ (x \ to (0)) \ frac (\ tg (x) - \ sin (x)) (x ^ 3) $.

Since $ \ lim_ (x \ to (0)) (\ tg (x) - \ sin (x)) = 0 $ (remember that $ \ sin (0) = \ tg (0) = 0 $) and $ \ lim_ (x \ to (0)) x ^ 3 = 0 $, then here we are dealing with an uncertainty of the form $ \ frac (0) (0) $. Let's open it as follows:

$$ \ lim_ (x \ to (0)) \ frac (\ tg (x) - \ sin (x)) (x ^ 3) = \ left | \ frac (0) (0) \ right | = \ lim_ (x \ to (0)) \ frac (\ frac (\ sin (x)) (\ cos (x)) - \ sin (x)) (x ^ 3) = \ lim_ (x \ to ( 0)) \ frac (\ sin (x) \ cdot \ left (\ frac (1) (\ cos (x)) - 1 \ right)) (x ^ 3) = \ lim_ (x \ to (0)) \ frac (\ sin (x) \ cdot \ left (1- \ cos (x) \ right)) (x ^ 3 \ cdot \ cos (x)) = \\ = \ lim_ (x \ to (0)) \ frac (\ sin (x) \ cdot (2) \ sin ^ 2 \ frac (x) (2)) (x ^ 3 \ cdot \ cos (x)) = \ frac (1) (2) \ cdot \ lim_ (x \ to (0)) \ left (\ frac (\ sin (x)) (x) \ cdot \ left (\ frac (\ sin \ frac (x) (2)) (\ frac (x) ( 2)) \ right) ^ 2 \ cdot \ frac (1) (\ cos (x)) \ right) = \ frac (1) (2) \ cdot (1) \ cdot (1 ^ 2) \ cdot (1 ) = \ frac (1) (2). $$

Answer: $ \ lim_ (x \ to (0)) \ frac (\ tg (x) - \ sin (x)) (x ^ 3) = \ frac (1) (2) $.

Example No. 9

Find the limit $ \ lim_ (x \ to (3)) \ frac (1- \ cos (x-3)) ((x-3) \ tg \ frac (x-3) (2)) $.

Since $ \ lim_ (x \ to (3)) (1- \ cos (x-3)) = 0 $ and $ \ lim_ (x \ to (3)) (x-3) \ tg \ frac (x -3) (2) = 0 $, then there is an uncertainty of the form $ \ frac (0) (0) $. Before proceeding to its expansion, it is convenient to replace the variable in such a way that the new variable tends to zero (note that the variable $ \ alpha \ to 0 $ in the formulas). The easiest way is to introduce the variable $ t = x-3 $. However, for the sake of convenience of further transformations (this benefit can be seen in the course of the solution below), it is worth making the following replacement: $ t = \ frac (x-3) (2) $. Note that both replacements are applicable in this case, just the second replacement will allow you to work less with fractions. Since $ x \ to (3) $, then $ t \ to (0) $.

$$ \ lim_ (x \ to (3)) \ frac (1- \ cos (x-3)) ((x-3) \ tg \ frac (x-3) (2)) = \ left | \ frac (0) (0) \ right | = \ left | \ begin (aligned) & t = \ frac (x-3) (2); \\ & t \ to (0) \ end (aligned) \ right | = \ lim_ (t \ to (0)) \ frac (1- \ cos (2t)) (2t \ cdot \ tg (t)) = \ lim_ (t \ to (0)) \ frac (2 \ sin ^ 2t) (2t \ cdot \ tg (t)) = \ lim_ (t \ to (0)) \ frac (\ sin ^ 2t) (t \ cdot \ tg (t)) = \\ = \ lim_ (t \ to (0)) \ frac (\ sin ^ 2t) (t \ cdot \ frac (\ sin (t)) (\ cos (t))) = \ lim_ (t \ to (0)) \ frac (\ sin (t) \ cos (t)) (t) = \ lim_ (t \ to (0)) \ left (\ frac (\ sin (t)) (t) \ cdot \ cos (t) \ right) = \ lim_ (t \ to (0)) \ frac (\ sin (t)) (t) \ cdot \ lim_ (t \ to (0)) \ cos (t) = 1 \ cdot (1) = 1. $$

Answer: $ \ lim_ (x \ to (3)) \ frac (1- \ cos (x-3)) ((x-3) \ tg \ frac (x-3) (2)) = 1 $.

Example No. 10

Find the Limit $ \ lim_ (x \ to \ frac (\ pi) (2)) \ frac (1- \ sin (x)) (\ left (\ frac (\ pi) (2) -x \ right) ^ 2 ) $.

Again we are dealing with $ \ frac (0) (0) $ uncertainty. Before proceeding to its expansion, it is convenient to change the variable in such a way that the new variable tends to zero (note that the variable $ \ alpha \ to (0) $ in the formulas). The easiest way is to enter the variable $ t = \ frac (\ pi) (2) -x $. Since $ x \ to \ frac (\ pi) (2) $, then $ t \ to (0) $:

$$ \ lim_ (x \ to \ frac (\ pi) (2)) \ frac (1- \ sin (x)) (\ left (\ frac (\ pi) (2) -x \ right) ^ 2) = \ left | \ frac (0) (0) \ right | = \ left | \ begin (aligned) & t = \ frac (\ pi) (2) -x; \\ & t \ to (0) \ end (aligned) \ right | = \ lim_ (t \ to (0)) \ frac (1- \ sin \ left (\ frac (\ pi) (2) -t \ right)) (t ^ 2) = \ lim_ (t \ to (0 )) \ frac (1- \ cos (t)) (t ^ 2) = \\ = \ lim_ (t \ to (0)) \ frac (2 \ sin ^ 2 \ frac (t) (2)) ( t ^ 2) = 2 \ lim_ (t \ to (0)) \ frac (\ sin ^ 2 \ frac (t) (2)) (t ^ 2) = 2 \ lim_ (t \ to (0)) \ frac (\ sin ^ 2 \ frac (t) (2)) (\ frac (t ^ 2) (4) \ cdot (4)) = \ frac (1) (2) \ cdot \ lim_ (t \ to ( 0)) \ left (\ frac (\ sin \ frac (t) (2)) (\ frac (t) (2)) \ right) ^ 2 = \ frac (1) (2) \ cdot (1 ^ 2 ) = \ frac (1) (2). $$

Answer: $ \ lim_ (x \ to \ frac (\ pi) (2)) \ frac (1- \ sin (x)) (\ left (\ frac (\ pi) (2) -x \ right) ^ 2) = \ frac (1) (2) $.

Example No. 11

Find the limits $ \ lim_ (x \ to \ frac (\ pi) (2)) \ frac (1- \ sin (x)) (\ cos ^ 2x) $, $ \ lim_ (x \ to \ frac (2 \ pi) (3)) \ frac (\ tg (x) + \ sqrt (3)) (2 \ cos (x) +1) $.

In this case, we don't have to use the first wonderful limit. Please note: both the first and the second limits contain only trigonometric functions and numbers. Often, in examples of this kind, it is possible to simplify the expression under the limit sign. In this case, after the above simplification and reduction of some factors, the uncertainty disappears. I gave this example with only one purpose: to show that the presence of trigonometric functions under the limit sign does not necessarily mean the application of the first remarkable limit.

Since $ \ lim_ (x \ to \ frac (\ pi) (2)) (1- \ sin (x)) = 0 $ (remember that $ \ sin \ frac (\ pi) (2) = 1 $ ) and $ \ lim_ (x \ to \ frac (\ pi) (2)) \ cos ^ 2x = 0 $ (remember that $ \ cos \ frac (\ pi) (2) = 0 $), then we have dealing with an uncertainty of the form $ \ frac (0) (0) $. However, this does not mean that we need to use the first remarkable limit. To disclose the uncertainty, it is enough to take into account that $ \ cos ^ 2x = 1- \ sin ^ 2x $:

$$ \ lim_ (x \ to \ frac (\ pi) (2)) \ frac (1- \ sin (x)) (\ cos ^ 2x) = \ left | \ frac (0) (0) \ right | = \ lim_ (x \ to \ frac (\ pi) (2)) \ frac (1- \ sin (x)) (1- \ sin ^ 2x) = \ lim_ (x \ to \ frac (\ pi) ( 2)) \ frac (1- \ sin (x)) ((1- \ sin (x)) (1+ \ sin (x))) = \ lim_ (x \ to \ frac (\ pi) (2) ) \ frac (1) (1+ \ sin (x)) = \ frac (1) (1 + 1) = \ frac (1) (2). $$

There is a similar solution in Demidovich's Reshebnik (No. 475). As for the second limit, as in the previous examples of this section, we have an uncertainty of the form $ \ frac (0) (0) $. Why does it arise? It arises because $ \ tg \ frac (2 \ pi) (3) = - \ sqrt (3) $ and $ 2 \ cos \ frac (2 \ pi) (3) = - 1 $. We use these values to transform expressions in the numerator and denominator. The purpose of our actions: write down the sum in the numerator and denominator in the form of a product. By the way, often within a similar view, it is convenient to change a variable, made in such a way that the new variable tends to zero (see, for example, examples # 9 or # 10 on this page). However, in this example, there is no sense in replacing, although, if desired, it is easy to change the variable $ t = x- \ frac (2 \ pi) (3) $.

$$ \ lim_ (x \ to \ frac (2 \ pi) (3)) \ frac (\ tg (x) + \ sqrt (3)) (2 \ cos (x) +1) = \ lim_ (x \ to \ frac (2 \ pi) (3)) \ frac (\ tg (x) + \ sqrt (3)) (2 \ cdot \ left (\ cos (x) + \ frac (1) (2) \ right )) = \ lim_ (x \ to \ frac (2 \ pi) (3)) \ frac (\ tg (x) - \ tg \ frac (2 \ pi) (3)) (2 \ cdot \ left (\ cos (x) - \ cos \ frac (2 \ pi) (3) \ right)) = \\ = \ lim_ (x \ to \ frac (2 \ pi) (3)) \ frac (\ frac (\ sin \ left (x- \ frac (2 \ pi) (3) \ right)) (\ cos (x) \ cos \ frac (2 \ pi) (3))) (- 4 \ sin \ frac (x + \ frac (2 \ pi) (3)) (2) \ sin \ frac (x- \ frac (2 \ pi) (3)) (2)) = \ lim_ (x \ to \ frac (2 \ pi) (3 )) \ frac (\ sin \ left (x- \ frac (2 \ pi) (3) \ right)) (- 4 \ sin \ frac (x + \ frac (2 \ pi) (3)) (2) \ sin \ frac (x- \ frac (2 \ pi) (3)) (2) \ cos (x) \ cos \ frac (2 \ pi) (3)) = \\ = \ lim_ (x \ to \ frac (2 \ pi) (3)) \ frac (2 \ sin \ frac (x- \ frac (2 \ pi) (3)) (2) \ cos \ frac (x- \ frac (2 \ pi) (3 )) (2)) (- 4 \ sin \ frac (x + \ frac (2 \ pi) (3)) (2) \ sin \ frac (x- \ frac (2 \ pi) (3)) (2) \ cos (x) \ cos \ frac (2 \ pi) (3)) = \ lim_ (x \ to \ frac (2 \ pi) (3)) \ frac (\ cos \ frac (x- \ frac (2 \ pi) (3)) (2)) (- 2 \ sin \ frac (x + \ frac (2 \ pi) (3)) (2) \ cos (x) \ cos \ frac (2 \ pi) (3 )) = \\ = \ frac (1) (- 2 \ cdot \ frac (\ sqrt (3)) (2) \ cdot \ left (- \ frac (1) (2) \ right) \ cdot \ left ( - \ frac (1) (2) \ right)) = - \ frac (4 ) (\ sqrt (3)). $$

As you can see, we didn't have to apply the first wonderful limit. Of course, this can be done if desired (see note below), but it is not necessary.

What would be the solution using the first wonderful limit? show \ hide

Using the first remarkable limit, we get:

$$ \ lim_ (x \ to \ frac (2 \ pi) (3)) \ frac (\ sin \ left (x- \ frac (2 \ pi) (3) \ right)) (- 4 \ sin \ frac (x + \ frac (2 \ pi) (3)) (2) \ sin \ frac (x- \ frac (2 \ pi) (3)) (2) \ cos (x) \ cos \ frac (2 \ pi ) (3)) = \\ = \ lim_ (x \ to \ frac (2 \ pi) (3)) \ left (\ frac (\ sin \ left (x- \ frac (2 \ pi) (3) \ right)) (x- \ frac (2 \ pi) (3)) \ cdot \ frac (1) (\ frac (\ sin \ frac (x- \ frac (2 \ pi) (3)) (2)) (\ frac (x- \ frac (2 \ pi) (3)) (2))) \ cdot \ frac (1) (- 2 \ sin \ frac (x + \ frac (2 \ pi) (3)) ( 2) \ cos (x) \ cos \ frac (2 \ pi) (3)) \ right) = 1 \ cdot (1) \ cdot \ frac (1) (- 2 \ cdot \ frac (\ sqrt (3) ) (2) \ cdot \ left (- \ frac (1) (2) \ right) \ cdot \ left (- \ frac (1) (2) \ right)) = - \ frac (4) (\ sqrt ( 3)). $$

Answer: $ \ lim_ (x \ to \ frac (\ pi) (2)) \ frac (1- \ sin (x)) (\ cos ^ 2x) = \ frac (1) (2) $, $ \ lim_ ( x \ to \ frac (2 \ pi) (3)) \ frac (\ tg (x) + \ sqrt (3)) (2 \ cos (x) +1) = - \ frac (4) (\ sqrt ( 3)) $.