Integration of the simplest (elementary) fractions. Integration of rational functions and the method of undefined coefficients

“A mathematician, like an artist or a poet, creates patterns. And if his patterns are more stable, it is only because they are composed of ideas ... Patterns of a mathematician, just like the patterns of an artist or a poet, must be beautiful; ideas, just like colors or words, must match. Beauty is the first requirement: there is no place in the world for ugly mathematics».

G.H. Hardy

In the first chapter, it was noted that there are antiderivatives of fairly simple functions that can no longer be expressed through elementary functions... In this regard, those classes of functions of which we can say for sure that their antiderivatives are elementary functions acquire great practical importance. This class of functions includes rational functions, representing the ratio of two algebraic polynomials. Many problems lead to the integration of rational fractions. Therefore, it is very important to be able to integrate such functions.

2.1.1. Fractional rational functions

Rational fraction(or fractional rational function) is the ratio of two algebraic polynomials:

where and are polynomials.

Recall that polynomial (polynomial, whole rational function) n-th degree is called a function of the form

where - real numbers. For example,

- polynomial of the first degree;

- a polynomial of the fourth degree, etc.

The rational fraction (2.1.1) is called correct if the degree is lower than the degree, i.e. n<m, otherwise the fraction is called wrong.

Any improper fraction can be represented as the sum of a polynomial (whole part) and a regular fraction (fractional part). Allocation of the whole and fractional parts of an irregular fraction can be done according to the rule of dividing polynomials by "corner".

Example 2.1.1. Highlight the whole and fractional parts of the following irregular rational fractions:

a) , b) .

Solution ... a) Using the “corner” division algorithm, we obtain

Thus, we get

.

b) Here we also use the “corner” division algorithm:

As a result, we get

.

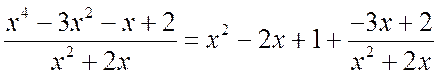Let's summarize. In general, the indefinite integral of a rational fraction can be represented as the sum of integrals of a polynomial and a regular rational fraction. Finding the antiderivatives of polynomials is not difficult. Therefore, in what follows we will mainly consider regular rational fractions.

2.1.2. The simplest rational fractions and their integration

Among the correct rational fractions, four types are distinguished, which are classified as the simplest (elementary) rational fractions:

where is an integer, , i.e. square trinomial has no valid roots.

Integration of the simplest fractions of the 1st and 2nd types is not very difficult:

, (2.1.3)

. (2.1.4)

Let us now consider the integration of the simplest fractions of the 3rd type, and we will not consider the fractions of the 4th type.

Let's start with integrals of the form

.

This integral is usually calculated by taking the full square in the denominator. The result is a tabular integral of the following form

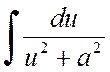or .

Example 2.1.2. Find integrals:

a) , b) .

Solution ... a) Let's select a complete square from a square trinomial:

From here we find

b) Having selected a complete square from a square trinomial, we get:

Thus,

.

To find the integral

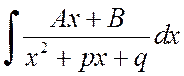
one can select the derivative of the denominator in the numerator and expand the integral into the sum of two integrals: the first of them by substitution comes down to the mind

,

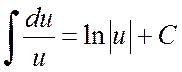and the second - to the one discussed above.

Example 2.1.3. Find integrals:

.

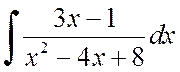Solution ... notice, that 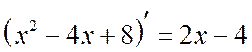... Select the derivative of the denominator in the numerator:

The first integral is calculated using the substitution :

In the second integral, select the complete square in the denominator

Finally, we get

2.1.3. Decomposition of a regular rational fraction
for the sum of the simplest fractions

Any correct rational fraction can be represented uniquely as a sum of simple fractions. To do this, the denominator must be factorized. It is known from higher algebra that every polynomial with real coefficients

As you know, any rational function of some variable x can be decomposed into a polynomial and the simplest, elementary, fractions. There are four types of simple fractions:
1) ;
2) ;
3) ;
4) .
Here a, A, B, b, c are real numbers. Equation x 2 + bx + c = 0 has no valid roots.

Integration of fractions of the first two types

Integration of the first two fractions is performed using the following formulas from the table of integrals:
,
, n ≠ - 1 .

1. Integration of a fraction of the first type

The fraction of the first type is reduced by the substitution t = x - a to a tabular integral:
.

2. Integration of a fraction of the second type

A fraction of the second type is reduced to a tabular integral by the same substitution t = x - a:

.

3. Integration of a fraction of the third type

Consider the integral of the third type of fraction:
.
We will calculate it in two steps.

3.1. Step 1. Select the derivative of the denominator in the numerator

Select the derivative of the denominator in the numerator of the fraction. We denote: u = x 2 + bx + c... Differentiate: u ′ = 2 x + b... Then
;
.
But
.
We have omitted the modulus sign because.

Then:
,
where
.

3.2. Step 2. Calculate the integral with A = 0, B = 1

Now we calculate the remaining integral:
.

We bring the denominator of the fraction to the sum of squares:
,
where .
We consider that the equation x 2 + bx + c = 0 has no roots. That's why .

Let's make a substitution
,
.
.

So,
.

Thus, we have found an integral of the third type of fraction:

,
where .

4. Integration of the fourth type of fraction

Finally, consider the integral of the fourth type of fraction:
.
We calculate it in three steps.

4.1) Select the derivative of the denominator in the numerator:
.

4.2) Calculate the integral
.

4.3) Calculate the integrals
,
using the cast formula:
.

4.1. Step 1. Selecting the derivative of the denominator in the numerator

Select the derivative of the denominator in the numerator, as we did in. Denote u = x 2 + bx + c... Differentiate: u ′ = 2 x + b... Then
.

.
But
.

Finally, we have:
.

4.2. Step 2. Calculation of the integral with n = 1

We calculate the integral
.
Its calculation is presented in.

4.3. Step 3. Derivation of the reduction formula

Now consider the integral
.

We bring the square trinomial to the sum of squares:
.
Here .
We make a substitution.
.
.

We perform transformations and integrate piece by piece.




.

Multiply by 2 (n - 1):
.
Back to x and I n.
,
;
;
.

So, for I n we got the reduction formula:
.
Applying this formula successively, we reduce the integral I n to I 1 .

Example

Calculate the integral

Solution

1. Select the derivative of the denominator in the numerator.
;
;


.
Here
.

2. We calculate the integral of the simplest fraction.

.

3. We apply the reduction formula:

for the integral.
In our case b = 1 , c = 1 , 4 c - b 2 = 3... We write out this formula for n = 2 and n = 3 :
;
.
From here

.

Finally, we have:

.
Find the coefficient at.
.

Here we provide detailed solutions for three examples of integrating the following rational fractions:
, , .

Example 1

Calculate the integral:
.

Solution

Here, under the integral sign stands a rational function, since the integrand is a fraction of polynomials. The degree of the denominator polynomial ( 3 ) is less than the degree of the numerator polynomial ( 4 ). Therefore, at first it is necessary to select the whole part of the fraction.

1. Let's select the whole part of the fraction. Divide x 4 by x 3 - 6 x 2 + 11 x - 6:

From here
.

2. Factor the denominator of the fraction. To do this, you need to solve the cubic equation:
.
6
1, 2, 3, 6, -1, -2, -3, -6 .
Substitute x = 1 :
.

1 ... Divide by x - 1 :

From here
.
Solving the quadratic equation.
.
Equation roots:,.
Then
.

3. Let us expand the fraction into elementary ones.

.

So we found:
.
We integrate.

Answer

Example 2

Calculate the integral:
.

Solution

Here, the numerator of the fraction is a polynomial of degree zero ( 1 = x 0). The denominator is a third degree polynomial. Insofar as 0 < 3 , then the fraction is correct. Let's decompose it into the simplest fractions.

1. Factor the denominator of the fraction. To do this, you need to solve the equation of the third degree:
.
Suppose it has at least one whole root. Then it is a divisor of the number 3 (term without x). That is, the whole root can be one of the numbers:
1, 3, -1, -3 .
Substitute x = 1 :
.

So, we found one root x = 1 ... Divide x 3 + 2 x - 3 on x - 1 :

So,
.

We solve the quadratic equation:
x 2 + x + 3 = 0.
Find the discriminant: D = 1 2 - 4 3 = -11... Since D< 0 , then the equation has no real roots. Thus, we got the factorization of the denominator:
.

2.
.
(x - 1) (x 2 + x + 3):
(2.1) .
Substitute x = 1 ... Then x - 1 = 0 ,
.

Substitute in (2.1) x = 0 :
1 = 3 A - C;
.

Let us equate in (2.1) coefficients at x 2 :
;
0 = A + B;
.

.

3. We integrate.
(2.2) .
To calculate the second integral, select the derivative of the denominator in the numerator and reduce the denominator to the sum of squares.

;
;
.

Calculate I 2 .


.
Since the equation x 2 + x + 3 = 0 has no real roots, then x 2 + x + 3> 0... Therefore, the modulus sign can be omitted.

We supply to (2.2) :
.

Answer

Example 3

Calculate the integral:
.

Solution

Here the integral is a fraction of polynomials. Therefore, the integrand is a rational function. The degree of the polynomial in the numerator is 3 ... The degree of the polynomial of the denominator of the fraction is 4 ... Insofar as 3 < 4 , then the fraction is correct. Therefore, it can be decomposed into the simplest fractions. But for this you need to factor the denominator.

1. Factor the denominator of the fraction. To do this, you need to solve the equation of the fourth degree:
.
Suppose it has at least one whole root. Then it is a divisor of the number 2 (term without x). That is, the whole root can be one of the numbers:
1, 2, -1, -2 .
Substitute x = -1 :
.

So, we found one root x = -1 ... Divide by x - (-1) = x + 1:


So,
.

Now you need to solve the equation of the third degree:
.
If we assume that this equation has an integer root, then it is a divisor of the number 2 (term without x). That is, the whole root can be one of the numbers:
1, 2, -1, -2 .
Substitute x = -1 :
.

So, we found another root x = -1 ... It would be possible, as in the previous case, to divide the polynomial by, but we will group the members:
.

Since the equation x 2 + 2 = 0 has no real roots, then we got the factorization of the denominator:
.

2. Let us expand the fraction into elementary ones. We are looking for a decomposition in the form:
.
Freed from the denominator of the fraction, multiply by (x + 1) 2 (x 2 + 2):
(3.1) .
Substitute x = -1 ... Then x + 1 = 0 ,
.

Differentiate (3.1) :

;

.
Substitute x = -1 and take into account that x + 1 = 0 :
;
; .

Substitute in (3.1) x = 0 :
0 = 2 A + 2 B + D;
.

Let us equate in (3.1) coefficients at x 3 :
;
1 = B + C;
.

So, we have found the decomposition into the simplest fractions:
.

3. We integrate.


.

TOPIC: Integration of rational fractions.

Attention! When studying one of the main methods of integration: the integration of rational fractions, it is required to consider polynomials in a complex domain to carry out rigorous proofs. Therefore it is necessary study in advance some properties of complex numbers and operations on them.

Integration of the simplest rational fractions.

If P(z) and Q(z) Are polynomials in the complex domain, then is a rational fraction. It is called correct if the degree P(z) less degree Q(z) , and wrong if the degree R not less than degree Q.

Any irregular fraction can be represented as: ,

P (z) = Q (z) S (z) + R (z),

a R(z) – polynomial less than degree Q(z).

Thus, the integration of rational fractions is reduced to the integration of polynomials, that is, power functions, and regular fractions, since it is a regular fraction.

Definition 5. The simplest (or elementary) fractions are fractions of the following types:

1) , 2) , 3) , 4) .

Let's find out how they are integrated.

3) (studied earlier).

Theorem 5. Any regular fraction can be represented as a sum of elementary fractions (without proof).

Corollary 1. If is a regular rational fraction, and if there are only simple real roots among the roots of the polynomial, then only the simplest fractions of the 1st type will be present in the expansion of the fraction into the sum of elementary fractions:

Example 1.

Corollary 2. If is a regular rational fraction, and if among the roots of the polynomial there are only multiple real roots, then in the expansion of the fraction into the sum of the simplest fractions there will be only the simplest fractions of the 1st and 2nd types:

Example 2.

Corollary 3. If is a regular rational fraction, and if among the roots of the polynomial there are only simple complex conjugate roots, then in the expansion of the fraction into the sum of the simplest fractions there will be only the simplest fractions of the third type:

Example 3.

Corollary 4. If is a regular rational fraction, and if among the roots of the polynomial there are only multiple complex conjugate roots, then the expansion of the fraction into the sum of simple fractions will contain only the simplest fractions of the 3rd and 4th types:

To determine the unknown coefficients in the given expansions, proceed as follows. The left and right sides of the decomposition containing unknown coefficients are multiplied by. It turns out that the two polynomials are equal. From it, equations for the desired coefficients are obtained using that:

1.equality is valid for any values ​​of X (method of particular values). In this case, as many equations as you like are obtained, any m of which make it possible to find unknown coefficients.

2. the coefficients coincide at the same powers of X (method of undefined coefficients). In this case, a system of m - equations with m - unknowns is obtained, from which unknown coefficients are found.

3. combined method.

Example 5. Expand a fraction into the simplest.

Solution:

Find the coefficients A and B.

Method 1 - the method of private values:

Method 2 - the method of undefined coefficients:

Answer:

Integration of rational fractions.

Theorem 6. Indefinite integral of any rational fraction on any interval on which its denominator is not is zero, exists and is expressed through elementary functions, namely rational fractions, logarithms and arctangents.

Proof.

We represent the rational fraction in the form: ... In this case, the last term is a regular fraction, and by Theorem 5 it can be represented as a linear combination of the simplest fractions. Thus, the integration of the rational fraction is reduced to the integration of the polynomial S(x) and the simplest fractions, the antiderivatives of which, as has been shown, have the form indicated in the theorem.

Comment. In this case, the main difficulty is the factorization of the denominator, that is, the search for all its roots.

Example 1. Find the integral

All of the above in the previous paragraphs allows us to formulate the basic rules for integrating a rational fraction.

1. If a rational fraction is incorrect, then it is represented as the sum of a polynomial and a regular rational fraction (see item 2).

By this, the integration of an irregular rational fraction is reduced to the integration of a polynomial and a regular rational fraction.

2. Factor the denominator of the correct fraction.

3. A regular rational fraction is decomposed into the sum of the simplest fractions. By this, the integration of the correct rational fraction is reduced to the integration of the simplest fractions.

Let's look at some examples.

Example 1. Find.

Solution. The integral is an irregular rational fraction. Separating the whole part, we get

Hence,

Noticing that, we expand the correct rational fraction

into simple fractions:

(see formula (18)). That's why

Thus, we finally have

Example 2. Find

Solution. The integral is a regular rational fraction.

Expanding it into simple fractions (see formula (16)), we obtain