Integration of a fractional-rational function.
Uncertain coefficient method

We continue to work on integrating fractions. We have already looked at integrals of some types of fractions in the lesson, and this lesson, in a sense, can be considered a continuation. To successfully understand the material, basic integration skills are required, so if you have just started studying integrals, that is, you are a beginner, then you need to start with the article Indefinite integral. Examples of solutions.

Oddly enough, now we will be engaged not so much in finding integrals, but... in solving systems of linear equations. In this regard urgently I recommend attending the lesson. Namely, you need to be well versed in substitution methods (“the school” method and the method of term-by-term addition (subtraction) of system equations).

What is a fractional rational function? In simple words, a fractional-rational function is a fraction whose numerator and denominator contain polynomials or products of polynomials. Moreover, the fractions are more sophisticated than those discussed in the article Integrating Some Fractions.

Integrating a Proper Fractional-Rational Function

Immediately an example and a typical algorithm for solving the integral of a fractional-rational function.

Example 1

Step 1. The first thing we ALWAYS do when solving an integral of a fractional rational function is to clarify the following question: is the fraction proper? This step is performed verbally, and now I will explain how:

First we look at the numerator and find out senior degree polynomial:

The leading power of the numerator is two.

Now we look at the denominator and find out senior degree denominator. The obvious way is to open the brackets and bring similar terms, but you can do it simpler, in each find the highest degree in brackets

and mentally multiply: - thus, the highest degree of the denominator is equal to three. It is quite obvious that if we actually open the brackets, we will not get a degree greater than three.

Conclusion: Major degree of numerator STRICTLY is less than the highest power of the denominator, which means the fraction is proper.

If in this example the numerator contained the polynomial 3, 4, 5, etc. degrees, then the fraction would be wrong.

Now we will consider only the correct fractional rational functions. The case when the degree of the numerator is greater than or equal to the degree of the denominator will be discussed at the end of the lesson.

Step 2. Let's factorize the denominator. Let's look at our denominator:

Generally speaking, this is already a product of factors, but, nevertheless, we ask ourselves: is it possible to expand something else? The object of torture will undoubtedly be the square trinomial. Solving the quadratic equation:

The discriminant is greater than zero, which means that the trinomial really can be factorized:

General rule: EVERYTHING that CAN be factored in the denominator - factor it

Let's begin to formulate a solution:

Step 3. Using the method of indefinite coefficients, we expand the integrand into a sum of simple (elementary) fractions. Now it will be clearer.

Let's look at our integrand function:

And, you know, somehow an intuitive thought pops up that it would be nice to turn our large fraction into several small ones. For example, like this:

The question arises, is it even possible to do this? Let us breathe a sigh of relief, the corresponding theorem of mathematical analysis states – IT IS POSSIBLE. Such a decomposition exists and is unique.

There's just one catch, the odds are Bye We don’t know, hence the name – the method of indefinite coefficients.

As you guessed, subsequent body movements are like that, don’t cackle! will be aimed at just RECOGNIZING them - to find out what they are equal to.

Be careful, I will explain in detail only once!

So, let's start dancing from:

On the left side we reduce the expression to a common denominator:

Now we can safely get rid of the denominators (since they are the same):

On the left side we open the brackets, but do not touch the unknown coefficients for now:

At the same time, we repeat the school rule of multiplying polynomials. When I was a teacher, I learned to pronounce this rule with a straight face: In order to multiply a polynomial by a polynomial, you need to multiply each term of one polynomial by each term of the other polynomial.

From the point of view of a clear explanation, it is better to put the coefficients in brackets (although I personally never do this in order to save time):

We compose a system of linear equations.
First we look for senior degrees:

And we write the corresponding coefficients into the first equation of the system:

Remember the following point well. What would happen if there were no s on the right side at all? Let's say, would it just show off without any square? In this case, in the equation of the system it would be necessary to put a zero on the right: . Why zero? But because on the right side you can always assign this same square with zero: If on the right side there are no variables and/or a free term, then we put zeros on the right sides of the corresponding equations of the system.

We write the corresponding coefficients into the second equation of the system:

And finally, mineral water, we select free members.

Eh...I was kind of joking. Jokes aside - mathematics is a serious science. In our institute group, no one laughed when the assistant professor said that she would scatter the terms along the number line and choose the largest ones. Let's get serious. Although... whoever lives to see the end of this lesson will still smile quietly.

The system is ready:

We solve the system:

(1) From the first equation we express and substitute it into the 2nd and 3rd equations of the system. In fact, it was possible to express (or another letter) from another equation, but in this case it is advantageous to express it from the 1st equation, since there the smallest odds.

(2) We present similar terms in the 2nd and 3rd equations.

(3) We add the 2nd and 3rd equations term by term, obtaining the equality , from which it follows that

(4) We substitute into the second (or third) equation, from where we find that

(5) Substitute and into the first equation, obtaining .

If you have any difficulties with the methods of solving the system, practice them in class. How to solve a system of linear equations?

After solving the system, it is always useful to check - substitute the found values every equation of the system, as a result everything should “converge”.

Almost there. The coefficients were found, and:

The finished job should look something like this:

As you can see, the main difficulty of the task was to compose (correctly!) and solve (correctly!) a system of linear equations. And at the final stage, everything is not so difficult: we use the linearity properties of the indefinite integral and integrate. Please note that under each of the three integrals we have a “free” complex function; I talked about the features of its integration in the lesson Variable change method in indefinite integral.

Check: Differentiate the answer:

The original integrand function has been obtained, which means that the integral has been found correctly.
During the verification, we had to reduce the expression to a common denominator, and this is not accidental. The method of indefinite coefficients and reducing an expression to a common denominator are mutually inverse actions.

Example 2

Find the indefinite integral.

Let's return to the fraction from the first example: . It is easy to notice that in the denominator all the factors are DIFFERENT. The question arises, what to do if, for example, the following fraction is given: ? Here we have degrees in the denominator, or, mathematically, multiples. In addition, there is a quadratic trinomial that cannot be factorized (it is easy to verify that the discriminant of the equation is negative, so the trinomial cannot be factorized). What to do? The expansion into a sum of elementary fractions will look something like with unknown coefficients at the top or something else?

Example 3

Introduce a function

Step 1. Checking if we have a proper fraction
Major numerator: 2
Highest degree of denominator: 8
, which means the fraction is correct.

Step 2. Is it possible to factor something in the denominator? Obviously not, everything is already laid out. The square trinomial cannot be expanded into a product for the reasons stated above. Hood. Less work.

Step 3. Let's imagine a fractional-rational function as a sum of elementary fractions.
In this case, the expansion has the following form:

Let's look at our denominator:
When decomposing a fractional-rational function into a sum of elementary fractions, three fundamental points can be distinguished:

1) If the denominator contains a “lonely” factor to the first power (in our case), then we put an indefinite coefficient at the top (in our case). Examples No. 1, 2 consisted only of such “lonely” factors.

2) If the denominator has multiple multiplier, then you need to decompose it like this:
- that is, sequentially go through all the degrees of “X” from the first to the nth degree. In our example there are two multiple factors: and , take another look at the expansion I gave and make sure that they are expanded exactly according to this rule.

3) If the denominator contains an indecomposable polynomial of the second degree (in our case), then when decomposing in the numerator you need to write a linear function with undetermined coefficients (in our case with undetermined coefficients and ).

In fact, there is another 4th case, but I will keep silent about it, since in practice it is extremely rare.

Example 4

Introduce a function as a sum of elementary fractions with unknown coefficients.

This is an example for you to solve on your own. Full solution and answer at the end of the lesson.
Follow the algorithm strictly!

If you understand the principles by which you need to expand a fractional-rational function into a sum, you can chew through almost any integral of the type under consideration.

Example 5

Find the indefinite integral.

Step 1. Obviously the fraction is correct:

Step 2. Is it possible to factor something in the denominator? Can. Here is the sum of cubes . Factor the denominator using the abbreviated multiplication formula

Step 3. Using the method of indefinite coefficients, we expand the integrand into a sum of elementary fractions:

Please note that the polynomial cannot be factorized (check that the discriminant is negative), so at the top we put a linear function with unknown coefficients, and not just one letter.

We bring the fraction to a common denominator:

Let's compose and solve the system:

(1) We express from the first equation and substitute it into the second equation of the system (this is the most rational way).

(2) We present similar terms in the second equation.

(3) We add the second and third equations of the system term by term.

All further calculations are, in principle, oral, since the system is simple.

(1) We write down the sum of fractions in accordance with the found coefficients.

(2) We use the linearity properties of the indefinite integral. What happened in the second integral? You can familiarize yourself with this method in the last paragraph of the lesson. Integrating Some Fractions.

(3) Once again we use the properties of linearity. In the third integral we begin to isolate the complete square (penultimate paragraph of the lesson Integrating Some Fractions).

(4) We take the second integral, in the third we select the complete square.

(5) Take the third integral. Ready.

“A mathematician, just like an artist or poet, creates patterns. And if his patterns are more stable, it is only because they are composed of ideas... The patterns of a mathematician, just like the patterns of an artist or a poet, must be beautiful; Ideas, just like colors or words, must correspond to each other. Beauty is the first requirement: there is no place in the world for ugly mathematics».

G.H.Hardy

In the first chapter it was noted that there are antiderivatives of fairly simple functions that can no longer be expressed through elementary functions. In this regard, those classes of functions about which we can accurately say that their antiderivatives are elementary functions acquire enormous practical importance. This class of functions includes rational functions, representing the ratio of two algebraic polynomials. Many problems lead to the integration of rational fractions. Therefore, it is very important to be able to integrate such functions.

2.1.1. Fractional rational functions

Rational fraction(or fractional rational function) is called the relation of two algebraic polynomials:

where and are polynomials.

Let us remind you that polynomial (polynomial, whole rational function) nth degree called a function of the form

Where – real numbers. For example,

– polynomial of the first degree;

– polynomial of the fourth degree, etc.

The rational fraction (2.1.1) is called correct, if the degree is lower than the degree , i.e. n<m, otherwise the fraction is called wrong.

Any improper fraction can be represented as the sum of a polynomial (the whole part) and a proper fraction (the fractional part). The separation of the whole and fractional parts of an improper fraction can be done according to the rule for dividing polynomials with a “corner”.

Example 2.1.1. Identify the whole and fractional parts of the following improper rational fractions:

A) , b) .

Solution . a) Using the “corner” division algorithm, we get

Thus, we get

.

b) Here we also use the “corner” division algorithm:

As a result, we get

.

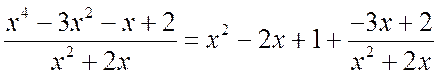Let's summarize. In the general case, the indefinite integral of a rational fraction can be represented as the sum of the integrals of the polynomial and the proper rational fraction. Finding antiderivatives of polynomials is not difficult. Therefore, in what follows we will mainly consider proper rational fractions.

2.1.2. The simplest rational fractions and their integration

Among proper rational fractions, there are four types, which are classified as the simplest (elementary) rational fractions:

3) ,

4) ,

where is an integer, , i.e. quadratic trinomial has no real roots.

Integrating simple fractions of the 1st and 2nd types does not present any great difficulties:

, (2.1.3)

. (2.1.4)

Let us now consider the integration of simple fractions of the 3rd type, but we will not consider fractions of the 4th type.

Let's start with integrals of the form

.

This integral is usually calculated by isolating the perfect square of the denominator. The result is a table integral of the following form

or .

Example 2.1.2. Find the integrals:

A) , b) .

Solution . a) Select a complete square from a quadratic trinomial:

From here we find

b) By isolating a complete square from a quadratic trinomial, we obtain:

Thus,

.

To find the integral

you can isolate the derivative of the denominator in the numerator and expand the integral into the sum of two integrals: the first of them by substitution comes down to appearance

,

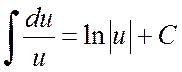and the second - to the one discussed above.

Example 2.1.3. Find the integrals:

.

Solution . notice, that 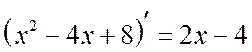. Let us isolate the derivative of the denominator in the numerator:

The first integral is calculated using the substitution :

In the second integral, we select the perfect square in the denominator

Finally, we get

2.1.3. Proper rational fraction expansion
for the sum of simple fractions

Any proper rational fraction can be represented in a unique way as a sum of simple fractions. To do this, the denominator must be factorized. From higher algebra it is known that every polynomial with real coefficients

One of the most important classes of functions, the integrals of which are expressed through elementary functions, is the class of rational functions.

Definition 1. Function of the form where
- polynomials of degreesnAndmcalled rational. An entire rational function, i.e. polynomial, integrates directly. The integral of a fractional-rational function can be found by decomposing into terms, which are converted in a standard way to the main tabular integrals.

Definition 2. Fraction
is called correct if the degree of the numeratornless than the power of the denominatorm. A fraction in which the degree of the numerator is greater than or equal to the degree of the denominator is called improper.

Any improper fraction can be represented as the sum of a polynomial and a proper fraction. This is done by dividing a polynomial by a polynomial, like dividing numbers.

Example.

Let's imagine a fraction
as the sum of a polynomial and a proper fraction:

x - 1

3

3

3

First term
in the quotient it is obtained as a result of dividing the leading term
, divided by the leading term X divider Then we multiply
per divisor x-1 and the resulting result is subtracted from the dividend; The remaining terms of the incomplete quotient are found similarly.

Having divided the polynomials, we get:

This action is called selecting a whole part.

Definition 3. The simplest fractions are proper rational fractions of the following types:

I.

II.
(K=2, 3, …).

III.
where is the square trinomial

IV.
where K=2, 3, …; quadratic trinomial
has no real roots.

a) expand the denominator
into the simplest real factors (according to the fundamental theorem of algebra, this expansion can contain linear binomials of the form
and quadratic trinomials
, having no roots);

b) write a diagram of the decomposition of a given fraction into the sum of simple fractions. Moreover, each factor of the form
corresponds k components of types I and II:

to each factor of the form
corresponds to e terms of types III and IV:

Example.

Write down the fraction expansion scheme
to the sum of the simplest.

c) perform the addition of the simplest fractions obtained. Write down the equality of the numerators of the resulting and original fractions;

d) find the coefficients of the corresponding expansion:
(solution methods will be discussed below);

e) substitute the found values ​​of the coefficients into the decomposition scheme.

Integrating any proper rational fraction after decomposition into its simplest terms reduces to finding integrals of one of the following types:

(k And e =2, 3, …).

Calculation of the integral reduces to formula III:

integral - to formula II:

integral can be found by the rule specified in the theory of integration of functions containing a quadratic trinomial; - through the transformations shown below in example 4.

Example 1.

a) factor the denominator:

b) write a diagram for decomposing the integrand into terms:

c) perform the addition of simple fractions:

Let us write down the equality of the numerators of the fractions:

d) there are two methods for finding unknown coefficients A, B, C.

Two polynomials are equal if and only if their coefficients are equal for the same powers X, so you can create the corresponding system of equations. This is one of the solution methods.

Coefficients at

free members (coefficient at ):4A=8.

Having solved the system, we get A=2, B=1, C= - 10.

Another method - private values ​​- will be discussed in the following example;

e) substitute the found values ​​into the decomposition scheme:

Substituting the resulting sum under the integral sign and integrating each term separately, we find:

Example 2.

Identity is an equality that is valid for any values ​​of the unknowns included in it. Based on this private value method. Can be given X any values. It is more convenient for calculations to take those values ​​that make any terms on the right side of the equality vanish.

Let x = 0. Then 1 = A 0(0+2)+V 0 (0-1)+С (0-1)(0+2).

Similarly for x = - 2 we have 1= - 2V*(-3), at x = 1 we have 1 = 3A.

Hence,

Example 3.

d) first we use the partial value method.

Let x = 0, Then 1 = A 1, A = 1.

At x = - 1 we have - 1+4+2+1 = - B(1+1+1) or 6 = - 3V, B = - 2.

To find the coefficients C and D, you need to create two more equations. For this you can take any other values X, For example x = 1 And x = 2. You can use the first method, i.e. equate coefficients at any identical powers X, for example when And . We get

1 = A+B+C and 4 = C +D- IN.

Knowing A = 1, B = -2, we'll find C = 2, D = 0 .

Thus, both methods can be combined when calculating coefficients.

Last integral we find separately according to the rule specified in the method of specifying a new variable. Let's select a perfect square in the denominator:

let's say
Then
We get:

=

Substituting into the previous equality, we find

Example 4.

Find

b)

d)

Integrating, we have:

Let us transform the first integral to formula III:

Let us transform the second integral to formula II:

In the third integral we replace the variable:

(When performing the transformations, we used the trigonometry formula

Find the integrals:

51.

52.

53.

54.

55.

56.

57.

58.

Self-test questions.

Which of these rational fractions are correct:

2. Is the diagram for decomposing a fraction into a sum of simple fractions written correctly?

A rational function is a fraction of the form , the numerator and denominator of which are polynomials or products of polynomials.

Example 1. Step 2.

.

We multiply the undetermined coefficients by polynomials that are not in this individual fraction, but which are in other resulting fractions:

We open the brackets and equate the numerator of the original integrand to the resulting expression:

In both sides of the equality, we look for terms with the same powers of x and compose a system of equations from them:

.

We cancel all the x’s and get an equivalent system of equations:

.

Thus, the final expansion of the integrand into a sum of simple fractions is:

.

Example 2. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

.

Now we begin to look for uncertain coefficients. To do this, we equate the numerator of the original fraction in the function expression to the numerator of the expression obtained after reducing the sum of fractions to a common denominator:

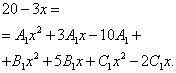
Now you need to create and solve a system of equations. To do this, we equate the coefficients of the variable to the corresponding degree in the numerator of the original expression of the function and similar coefficients in the expression obtained at the previous step:

We solve the resulting system:

So, from here

.

Example 3. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

We begin to look for uncertain coefficients. To do this, we equate the numerator of the original fraction in the function expression to the numerator of the expression obtained after reducing the sum of fractions to a common denominator:

As in previous examples, we compose a system of equations:

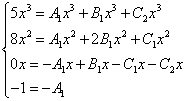
We reduce the x's and get an equivalent system of equations:

Solving the system, we obtain the following values ​​of the uncertain coefficients:

We obtain the final decomposition of the integrand into the sum of simple fractions:

.

Example 4. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

.

We already know from previous examples how to equate the numerator of the original fraction with the expression in the numerator obtained after decomposing the fraction into the sum of simple fractions and bringing this sum to a common denominator. Therefore, just for control purposes, we present the resulting system of equations:

Solving the system, we obtain the following values ​​of the uncertain coefficients:

We obtain the final decomposition of the integrand into the sum of simple fractions:

Example 5. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

.

We independently reduce this sum to a common denominator, equating the numerator of this expression to the numerator of the original fraction. The result should be the following system of equations:

Solving the system, we obtain the following values ​​of the uncertain coefficients:

.

We obtain the final decomposition of the integrand into the sum of simple fractions:

.

Example 6. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

We perform the same actions with this amount as in the previous examples. The result should be the following system of equations:

Solving the system, we obtain the following values ​​of the uncertain coefficients:

.

We obtain the final decomposition of the integrand into the sum of simple fractions:

.

Example 7. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

.

After certain actions with the resulting amount, the following system of equations should be obtained:

Solving the system, we obtain the following values ​​of the uncertain coefficients:

We obtain the final decomposition of the integrand into the sum of simple fractions:

.

Example 8. Step 2. At step 1, we obtained the following decomposition of the original fraction into the sum of simple fractions with undetermined coefficients in the numerators:

.

Let's make some changes to the actions that have already been brought to automaticity to obtain a system of equations. There is an artificial technique that in some cases helps to avoid unnecessary calculations. Bringing the sum of fractions to a common denominator, we obtain and equating the numerator of this expression to the numerator of the original fraction, we obtain.

A test on the integration of functions, including rational fractions, is given to 1st and 2nd year students. Examples of integrals will mainly be of interest to mathematicians, economists, and statisticians. These examples were asked during the test at LNU. I. Frank. The conditions of the following examples are “Find the integral” or “Calculate the integral”, so to save space and your time they were not written out.

Example 15. We came to the integration of fractional-rational functions. They occupy a special place among integrals because they require a lot of time to calculate and help teachers test your knowledge not only of integration. To simplify the function under the integral, we add and subtract an expression in the numerator that will allow us to split the function under the integral into two simple ones

As a result, we find one integral quite quickly, in the second we need to expand the fraction into a sum of elementary fractions

When reduced to a common denominator, we obtain the following numerals

Next, open the brackets and group

We equate the value for the same powers of “x” on the right and left. As a result, we arrive at a system of three linear equations (SLAE) with three unknowns.

How to solve systems of equations is described in other articles on the site. In the final version you will receive the following SLAE solution
A=4; B=-9/2; C=-7/2.
We substitute constants into the expansion of fractions into simple ones and perform integration


This concludes the example.

Example 16. Again we need to find the integral of a fractional rational function. To begin with, we will decompose the cubic equation contained in the denominator of the fraction into simple factors

Next, we decompose the fraction into its simplest forms

We reduce the right side to a common denominator and open the brackets in the numerator.


We equate the coefficients for the same degrees of the variable. Let's come to the SLAE again with three unknowns

We substitute the values ​​of A, B, C into the expansion and calculate the integral

The first two terms give the logarithm, the last one is also easy to find.

Example 17. In the denominator of the fractional rational function we have the difference of cubes. Using abbreviated multiplication formulas, we decompose it into two simple factors

Next, we write the resulting fractional function into the sum of simple fractions and reduce them to a common denominator

In the numerator we get the following expression.

From it we form a system of linear equations to calculate 3 unknowns

A=1/3; B=-1/3; C=1/3.
We substitute A, B, C into the formula and perform integration. As a result, we arrive at the following answer:


Here the numerator of the second integral was converted into a logarithm, and the remainder under the integral gives the arctangent.
There are a lot of similar examples on the integration of rational fractions on the Internet. You can find similar examples from the materials below.