Solve the system using the inverse matrix method online calculator. inverse matrix

System m linear equations with n unknowns called a system of the form

where aij And b i (i=1,…,m; b=1,…,n) are some known numbers, and x 1 ,…,x n- unknown. In the notation of the coefficients aij first index i denotes the number of the equation, and the second j is the number of the unknown at which this coefficient stands.

The coefficients for the unknowns will be written in the form of a matrix , which we will call system matrix.

The numbers on the right sides of the equations b 1 ,…,b m called free members.

Aggregate n numbers c 1 ,…,c n called decision of this system, if each equation of the system becomes an equality after substituting numbers into it c 1 ,…,c n instead of the corresponding unknowns x 1 ,…,x n.

Our task will be to find solutions to the system. In this case, three situations may arise:

A system of linear equations that has at least one solution is called joint. Otherwise, i.e. if the system has no solutions, then it is called incompatible.

Consider ways to find solutions to the system.

MATRIX METHOD FOR SOLVING SYSTEMS OF LINEAR EQUATIONS

Matrices make it possible to briefly write down a system of linear equations. Let a system of 3 equations with three unknowns be given:

Consider the matrix of the system 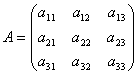and matrix columns of unknown and free members

Let's find the product

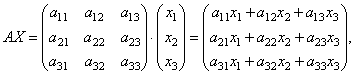
those. as a result of the product, we obtain the left-hand sides of the equations of this system. Then using the definition of matrix equality this system can be written in the form

or shorter A∙X=B.

Here matrices A And B are known, and the matrix X unknown. She needs to be found, because. its elements are the solution of this system. This equation is called matrix equation.

Let the matrix determinant be different from zero | A| ≠ 0. Then the matrix equation is solved as follows. Multiply both sides of the equation on the left by the matrix A-1, the inverse of the matrix A: . Insofar as A -1 A = E And E∙X=X, then we obtain the solution of the matrix equation in the form X = A -1 B .

Note that since the inverse matrix can only be found for square matrices, then the matrix method can solve only those systems in which the number of equations is the same as the number of unknowns. However, the matrix notation of the system is also possible in the case when the number of equations is not equal to the number of unknowns, then the matrix A is not square and therefore it is impossible to find a solution to the system in the form X = A -1 B.

Examples. Solve systems of equations.

CRAMER'S RULE

Consider a system of 3 linear equations with three unknowns:

Third-order determinant corresponding to the matrix of the system, i.e. composed of coefficients at unknowns,

called system determinant.

We compose three more determinants as follows: we replace successively 1, 2 and 3 columns in the determinant D with a column of free terms

Then we can prove the following result.

Theorem (Cramer's rule). If the determinant of the system is Δ ≠ 0, then the system under consideration has one and only one solution, and

Proof. So, consider a system of 3 equations with three unknowns. Multiply the 1st equation of the system by the algebraic complement A 11 element a 11, 2nd equation - on A21 and 3rd - on A 31:

Let's add these equations:

Consider each of the brackets and right side this equation. By the theorem on the expansion of the determinant in terms of the elements of the 1st column

Similarly, it can be shown that and .

Finally, it is easy to see that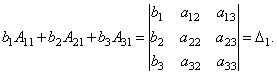

Thus, we get the equality: .

Consequently, .

The equalities and are derived similarly, whence the assertion of the theorem follows.

Thus, we note that if the determinant of the system is Δ ≠ 0, then the system has only decision and back. If the determinant of the system zero, then the system either has an infinite set of solutions or has no solutions, i.e. incompatible.

Examples. Solve a system of equations

GAUSS METHOD

The previously considered methods can be used to solve only those systems in which the number of equations coincides with the number of unknowns, and the determinant of the system must be different from zero. The Gaussian method is more universal and is suitable for systems with any number of equations. It consists in the successive elimination of unknowns from the equations of the system.

Consider again the system three equations with three unknowns:

.

We leave the first equation unchanged, and from the 2nd and 3rd we exclude the terms containing x 1. To do this, we divide the second equation by but 21 and multiply by - but 11 and then add with the 1st equation. Similarly, we divide the third equation into but 31 and multiply by - but 11 and then add it to the first one. As a result, the original system will take the form:

Now, from the last equation, we eliminate the term containing x2. To do this, divide the third equation by , multiply by and add it to the second. Then we will have a system of equations:

Hence from the last equation it is easy to find x 3, then from the 2nd equation x2 and finally from the 1st - x 1.

When using the Gaussian method, the equations can be interchanged if necessary.

Often instead of writing new system equations are limited to writing out the extended matrix of the system:

and then bring it to a triangular or diagonal form using elementary transformations.

TO elementary transformations matrices include the following transformations:

1. permutation of rows or columns;
2. multiplying a string by a non-zero number;
3. adding to one line other lines.

Examples: Solve systems of equations using the Gauss method.

Thus, the system has an infinite number of solutions.

This is a concept that generalizes all possible operations performed with matrices. Mathematical matrix - a table of elements. About a table where m lines and n columns, they say that this matrix has the dimension m on the n.

General view of the matrix:

For matrix solutions you need to understand what a matrix is ​​​​and know its main parameters. The main elements of the matrix:

• Main Diagonal Consisting of Elements a 11, a 22 ..... a mn.
• Side diagonal consisting of elements а 1n ,а 2n-1 …..а m1.

The main types of matrices:

• Square - such a matrix, where the number of rows = the number of columns ( m=n).
• Zero - where all elements of the matrix = 0.
• Transposed Matrix - Matrix IN, which was obtained from the original matrix A by replacing rows with columns.
• Single - all elements of the main diagonal = 1, all others = 0.
• An inverse matrix is ​​a matrix that, when multiplied by the original matrix, results in the identity matrix.

The matrix can be symmetrical with respect to the main and secondary diagonals. That is, if a 12 = a 21, a 13 \u003d a 31, .... a 23 \u003d a 32 .... a m-1n =a mn-1, then the matrix is ​​symmetric with respect to the main diagonal. Only square matrices can be symmetric.

Methods for solving matrices.

Almost all matrix solution methods are to find its determinant n th order and most of them are quite cumbersome. To find the determinant of the 2nd and 3rd order, there are other, more rational ways.

Finding determinants of the 2nd order.

To calculate the matrix determinant BUT 2nd order, it is necessary to subtract the product of the elements of the secondary diagonal from the product of the elements of the main diagonal:

Methods for finding determinants of the 3rd order.

Below are the rules for finding the 3rd order determinant.

Simplified the triangle rule as one of matrix solution methods, can be represented as follows:

In other words, the product of elements in the first determinant that are connected by lines is taken with a "+" sign; also, for the 2nd determinant - the corresponding products are taken with the "-" sign, that is, according to the following scheme:

At solving matrices by the Sarrus rule, to the right of the determinant, the first 2 columns are added and the products of the corresponding elements on the main diagonal and on the diagonals that are parallel to it are taken with a "+" sign; and the products of the corresponding elements of the secondary diagonal and the diagonals that are parallel to it, with the sign "-":

Row or column expansion of determinant when solving matrices.

The determinant is equal to the sum of the products of the elements of the row of the determinant and their algebraic complements. Usually choose the row/column in which/th there are zeros. The row or column on which the decomposition is carried out will be indicated by an arrow.

Reducing the determinant to a triangular form when solving matrices.

At solving matrices By reducing the determinant to a triangular form, they work like this: using the simplest transformations on rows or columns, the determinant becomes triangular and then its value, in accordance with the properties of the determinant, will be equal to the product of the elements that stand on the main diagonal.

Laplace's theorem for solving matrices.

When solving matrices using Laplace's theorem, it is necessary to know the theorem itself directly. Laplace's theorem: Let Δ is a determinant n-th order. We select any k rows (or columns), provided k≤ n - 1. In this case, the sum of the products of all minors k th order contained in the selected k rows (columns), their algebraic additions will be equal to the determinant.

Inverse matrix solution.

Sequence of actions for solutions inverse matrix :

1. Find out if the given matrix is ​​square. In the case of a negative answer, it becomes clear that there cannot be an inverse matrix for it.
2. We calculate algebraic additions.
3. We compose the allied (mutual, attached) matrix C.
4. We compose an inverse matrix from algebraic additions: all elements of the adjoint matrix C divide by the determinant of the initial matrix. The resulting matrix will be the desired inverse matrix with respect to the given one.
5. We check the work done: we multiply the matrix of the initial and resulting matrices, the result should be identity matrix.

Solution of matrix systems.

For solutions of matrix systems most commonly used is the Gauss method.

The Gauss method is a standard way to solve systems of linear algebraic equations(SLAE) and it lies in the fact that the variables are sequentially excluded, i.e., with the help of elementary changes, the system of equations is brought to an equivalent system of a triangular type and from it, sequentially, starting from the last (by number), each element of the system is found.

Gauss method is the most versatile and the best tool to find the solution of matrices. If the system has an infinite number of solutions or the system is incompatible, then it cannot be solved using Cramer's rule and the matrix method.

The Gauss method also implies direct (reduction of the extended matrix to a stepped form, i.e. getting zeros under the main diagonal) and reverse (getting zeros over the main diagonal of the extended matrix) moves. The forward move is the Gauss method, the reverse is the Gauss-Jordan method. The Gauss-Jordan method differs from the Gauss method only in the sequence of elimination of variables.

Let there be a square matrix of the nth order

Matrix A -1 is called inverse matrix with respect to the matrix A, if A * A -1 = E, where E is the identity matrix of the nth order.

Identity matrix- such a square matrix, in which all elements along the main diagonal, passing from the upper left corner to the lower right corner, are ones, and the rest are zeros, for example:

inverse matrix may exist only for square matrices those. for those matrices that have the same number of rows and columns.

Inverse Matrix Existence Condition Theorem

For a matrix to have an inverse matrix, it is necessary and sufficient that it be nondegenerate.

The matrix A = (A1, A2,...A n) is called non-degenerate if the column vectors are linearly independent. The number of linearly independent column vectors of a matrix is ​​called the rank of the matrix. Therefore, we can say that in order for an inverse matrix to exist, it is necessary and sufficient that the rank of the matrix is ​​equal to its dimension, i.e. r = n.

Algorithm for finding the inverse matrix

1. Write the matrix A in the table for solving systems of equations by the Gauss method and on the right (in place of the right parts of the equations) assign matrix E to it.
2. Using Jordan transformations, bring matrix A to a matrix consisting of single columns; in this case, it is necessary to simultaneously transform the matrix E.
3. If necessary, rearrange the rows (equations) of the last table so that the identity matrix E is obtained under the matrix A of the original table.
4. Write the inverse matrix A -1, which is in the last table under the matrix E of the original table.

Example 1

For matrix A, find the inverse matrix A -1

Solution: We write down the matrix A and on the right we assign the identity matrix E. Using Jordan transformations, we reduce the matrix A to the identity matrix E. The calculations are shown in Table 31.1.

Let's check the correctness of the calculations by multiplying the original matrix A and the inverse matrix A -1.

As a result of matrix multiplication, the identity matrix is ​​obtained. Therefore, the calculations are correct.

Answer:

Solution of matrix equations

Matrix equations can look like:

AX = B, XA = B, AXB = C,

where A, B, C are given matrices, X is the desired matrix.

Matrix equations are solved by multiplying the equation by inverse matrices.

For example, to find the matrix from an equation, you need to multiply this equation by on the left.

Therefore, to find a solution to the equation, you need to find the inverse matrix and multiply it by the matrix on the right side of the equation.

Other equations are solved similarly.

Example 2

Solve the equation AX = B if

Solution: Since the inverse of the matrix equals (see example 1)

Matrix method in economic analysis

Along with others, they also find application matrix methods. These methods are based on linear and vector-matrix algebra. Such methods are used for the purposes of analyzing complex and multidimensional economic phenomena. Most often, these methods are used when it is necessary to compare the functioning of organizations and their structural divisions.

In the process of applying matrix methods of analysis, several stages can be distinguished.

At the first stage the formation of a system of economic indicators is carried out and on its basis a matrix of initial data is compiled, which is a table in which system numbers are shown in its individual lines (i = 1,2,....,n), and along the vertical graphs - numbers of indicators (j = 1,2,....,m).

At the second stage for each vertical column, the largest of the available values ​​of the indicators is revealed, which is taken as a unit.

After that, all the amounts reflected in this column are divided by the largest value and a matrix of standardized coefficients is formed.

At the third stage all components of the matrix are squared. If they have different significance, then each indicator of the matrix is ​​assigned a certain weighting coefficient k. The value of the latter is determined by an expert.

On the last fourth stage found values ​​of ratings Rj grouped in order of increasing or decreasing.

The above matrix methods should be used, for example, when comparative analysis various investment projects, as well as in assessing other economic performance indicators of organizations.

(sometimes this method is also called the matrix method or the inverse matrix method) requires prior familiarization with such a concept as the matrix form of writing SLAE. The inverse matrix method is intended for solving those systems of linear algebraic equations for which the system matrix determinant is nonzero. Naturally, this implies that the matrix of the system is square (the concept of determinant exists only for square matrices). The essence of the inverse matrix method can be expressed in three points:

1. Write down three matrices: the system matrix $A$, the matrix of unknowns $X$, the matrix of free terms $B$.
2. Find the inverse matrix $A^(-1)$.
3. Using the equality $X=A^(-1)\cdot B$ get the solution of the given SLAE.

Any SLAE can be written in matrix form as $A\cdot X=B$, where $A$ is the matrix of the system, $B$ is the matrix of free terms, $X$ is the matrix of unknowns. Let the matrix $A^(-1)$ exist. Multiply both sides of the equality $A\cdot X=B$ by the matrix $A^(-1)$ on the left:

$$A^(-1)\cdot A\cdot X=A^(-1)\cdot B.$$

Since $A^(-1)\cdot A=E$ ($E$ is the identity matrix), then the equality written above becomes:

$$E\cdot X=A^(-1)\cdot B.$$

Since $E\cdot X=X$, then:

$$X=A^(-1)\cdot B.$$

Example #1

Solve the SLAE $ \left \( \begin(aligned) & -5x_1+7x_2=29;\\ & 9x_1+8x_2=-11. \end(aligned) \right.$ using the inverse matrix.

$$ A=\left(\begin(array) (cc) -5 & 7\\ 9 & 8 \end(array)\right);\; B=\left(\begin(array) (c) 29\\ -11 \end(array)\right);\; X=\left(\begin(array) (c) x_1\\ x_2 \end(array)\right). $$

Let's find the inverse matrix to the matrix of the system, i.e. calculate $A^(-1)$. In example #2

$$ A^(-1)=-\frac(1)(103)\cdot\left(\begin(array)(cc) 8 & -7\\ -9 & -5\end(array)\right) . $$

Now let's substitute all three matrices ($X$, $A^(-1)$, $B$) into the equation $X=A^(-1)\cdot B$. Then we perform matrix multiplication

$$ \left(\begin(array) (c) x_1\\ x_2 \end(array)\right)= -\frac(1)(103)\cdot\left(\begin(array)(cc) 8 & -7\\ -9 & -5\end(array)\right)\cdot \left(\begin(array) (c) 29\\ -11 \end(array)\right)=\\ =-\frac (1)(103)\cdot \left(\begin(array) (c) 8\cdot 29+(-7)\cdot (-11)\\ -9\cdot 29+(-5)\cdot (- 11) \end(array)\right)= -\frac(1)(103)\cdot \left(\begin(array) (c) 309\\ -206 \end(array)\right)=\left( \begin(array) (c) -3\\ 2\end(array)\right). $$

So we got $\left(\begin(array) (c) x_1\\ x_2 \end(array)\right)=\left(\begin(array) (c) -3\\ 2\end(array )\right)$. From this equality we have: $x_1=-3$, $x_2=2$.

Answer: $x_1=-3$, $x_2=2$.

Example #2

Solve SLAE $ \left\(\begin(aligned) & x_1+7x_2+3x_3=-1;\\ & -4x_1+9x_2+4x_3=0;\\ & 3x_2+2x_3=6. \end(aligned)\right .$ by the inverse matrix method.

Let us write down the matrix of the system $A$, the matrix of free terms $B$ and the matrix of unknowns $X$.

$$ A=\left(\begin(array) (ccc) 1 & 7 & 3\\ -4 & 9 & 4 \\0 & 3 & 2\end(array)\right);\; B=\left(\begin(array) (c) -1\\0\\6\end(array)\right);\; X=\left(\begin(array) (c) x_1\\ x_2 \\ x_3 \end(array)\right). $$

Now it's time to find the inverse matrix of the system matrix, i.e. find $A^(-1)$. In example #3 on the page dedicated to finding inverse matrices, the inverse matrix has already been found. Let's use the finished result and write $A^(-1)$:

$$ A^(-1)=\frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & - 3 & 37\end(array)\right). $$

Now we substitute all three matrices ($X$, $A^(-1)$, $B$) into the equality $X=A^(-1)\cdot B$, after which we perform matrix multiplication on the right side of this equality.

$$ \left(\begin(array) (c) x_1\\ x_2 \\ x_3 \end(array)\right)= \frac(1)(26)\cdot \left(\begin(array) (ccc) 6 & -5 & 1 \\ 8 & 2 & -16 \\ -12 & -3 & 37\end(array) \right)\cdot \left(\begin(array) (c) -1\\0\ \6\end(array)\right)=\\ =\frac(1)(26)\cdot \left(\begin(array) (c) 6\cdot(-1)+(-5)\cdot 0 +1\cdot 6 \\ 8\cdot (-1)+2\cdot 0+(-16)\cdot 6 \\ -12\cdot (-1)+(-3)\cdot 0+37\cdot 6 \end(array)\right)=\frac(1)(26)\cdot \left(\begin(array) (c) 0\\-104\\234\end(array)\right)=\left( \begin(array) (c) 0\\-4\\9\end(array)\right) $$

So we got $\left(\begin(array) (c) x_1\\ x_2 \\ x_3 \end(array)\right)=\left(\begin(array) (c) 0\\-4\ \9\end(array)\right)$. From this equality we have: $x_1=0$, $x_2=-4$, $x_3=9$.