Parallel transfer.

Transfer along the ordinate axis

f (x) \u003d\u003e f (x) - b
Let it be necessary to construct a graph of the function y \u003d f (x) - b. It is easy to note that the ordents of this schedule for all values \u200b\u200bx on | b | units less than the respective ordents of the graph of functions y \u003d f (x) at b\u003e 0 and on | b | Units are greater - with B 0 or up with B to construct a graph of the function y + b \u003d f (x), a graph of the function y \u003d f (x) should be constructed and transfer the abscissa axis to | B | units up with b\u003e 0 or on | b | units down when b

Transfer along the abscissa axis

f (x) \u003d\u003e f (x + a)
Let it be required to construct a graph of the function y \u003d f (x + a). Consider the function y \u003d f (x), which at some point x \u003d x1 takes the value u1 \u003d f (x1). Obviously, the function y \u003d f (x + a) will take the same value at the point x2, the coordinate of which is determined from the equality x2 + a \u003d x1, i.e. x2 \u003d x1 - a, and the equality in question is valid for the set of all values \u200b\u200bfrom the function of determining the function. Consequently, the graph of the function y \u003d f (x + a) can be obtained by parallel movement of the function of the function y \u003d f (x) along the abscissa axis to the left on | A | units at a\u003e 0 or right on | A | units with a to construct a graph function y \u003d f (x + a) should construct a function of the function y \u003d f (x) and transfer the ordinate axis | a | units to the right at a\u003e 0 or on | a | units left at a

Examples:

1.y \u003d f (x + a)

2.y \u003d f (x) + b

Reflection.

Construction of the graph of the function of the form y \u003d f (-X)

f (x) \u003d\u003e f (-x)
It is obvious that the functions y \u003d f (-x) and y \u003d f (x) take equal values \u200b\u200bat points, the abscissions of which are equal in absolute value, but are opposed to the sign. In other words, the orders of the graphics of the function y \u003d f (-x) in the area of \u200b\u200bpositive (negative) values \u200b\u200bwill be equal to the order of the graph function y \u003d f (x) with the negative (positive) values \u200b\u200bof x. Thus, we obtain the following rule.
To build a graph of the function Y \u003d F (-X), a graph of the function y \u003d f (x) should be constructed and reflect it relative to the ordinate axis. The resulting schedule is a graph of the function Y \u003d F (-X)

Construction of the graph of the function of the form y \u003d - f (x)

f (x) \u003d\u003e - f (x)
The claims of the graph of the function y \u003d - f (x) with all values \u200b\u200bof the argument are equal in absolute value, but are opposite to the signatam signatures of the function y \u003d f (x) with the same values \u200b\u200bof the argument. Thus, we obtain the following rule.
To build a graph of the function y \u003d - f (x), a graph of the function y \u003d f (x) should be constructed and reflect it relative to the abscissa axis.

Examples:

1.y \u003d -f (x)

2.y \u003d F (-X)

3.y \u003d -F (-X)

Deformation.

Deformation of the schedule along the ordinate axis

f (x) \u003d\u003e k f (x)
Consider the function of the form y \u003d kf (x), where k\u003e 0. It is easy to see that with equal values \u200b\u200bof the argument values, the claims of this function will be in the k times more the ordents of the function of the function y \u003d f (x) at k\u003e 1 or 1 / k less than the ordinate graphics of the function y \u003d f (x) for k to construct the function of the Y \u003d KF (x) graphics of the function y \u003d f (x) and increase its ordinates in K\u003e 1 (to stretch the chart along the ordinate axis ) or reduce its ordines in 1 / k times when
k\u003e 1. - stretching from the axis oh
0 - compression to OX axis

Deformation of the schedule along the abscissa axis

f (x) \u003d\u003e f (k x)
Let it be necessary to construct a graph of the function y \u003d f (kx), where k\u003e 0. Consider the function y \u003d f (x), which in an arbitrary point x \u003d x1 takes the value y1 \u003d f (x1). Obviously, the function y \u003d f (kx) takes the same value at the point x \u003d x2, the coordinate of which is determined by the equality x1 \u003d kx2, and this equality is valid for the combination of all values \u200b\u200bx from the function of determining the function. Consequently, the graph of the function y \u003d f (kx) is compressed (at k 1) along the abscissa axis relative to the graph of the function y \u003d f (x). Thus, we receive the rule.
To build a graph of the function y \u003d f (kx), a graph of the function y \u003d f (x) should be constructed and reduce its abscissa in K\u003e 1 (to compress the graph along the abscissa axis) or increase its abscissa in 1 / k times when
k\u003e 1. - compression to the OU axis
0 - stretching from Oy axis

from π to 3π / 2, SIN x decreases from 0 to -1, and when X increases from 3π / 2 to 2π, it increases from -1 to 0. So, the graph of the graph for 0 6 x 6 2π is ready (Fig. 11.2 B ). Note, by the way, that the curve on Fig11.2 and is symmetrical with respect to the vertical direct with the equation x \u003d π / 2. In fact, the formula of bringing Sin (π / 2 - x) \u003d SIN x shows that the points with the abscissions x and π - x have the same ordinates on the chart and, it became symmetrical with respect to direct x \u003d π / 2 (Fig. 11.3 but).

Task 11.1. Record the equation of direct concerning the graph of the function y \u003d sin x at the point with coordinates (π; 0).

The curve in Fig. 11.2 B is centrally symmetric about the point with coordinates (π; 0); This follows from another formula of bringing: sin (2π - x) \u003d - sin x (Fig.11.3 b).

After we have a portion of the function of the function y \u003d sin x for 0 6 x 6 2π, the entire schedule is already built simply. In fact, when the end of the arrow passed the way 2π, the arrow returned to its original position; With further movement, everything will be repeated. So, the schedule will consist of the same pieces as in Fig. 11.2 b. The final graph of the function y \u003d sin x looks like in Fig.16.4. At the same time, the plots of graphics at x ,, [-2π; 0],. . . It is obtained from the graph in Figs11.2 B shift along the abscissa axis by 2π, 4π, -2π,. . . respectively. This is simply reformulating the fact that the Y \u003d SIN X function has a period of 2π.

Fig. 11.4. y \u003d sin x.

Fig. 11.5. y \u003d cos x.

Now we construct the graph of the function y \u003d cos x. It would be possible to build it just as we built a sinus graph. We, however, choose another path that will allow you to use our information already exist.

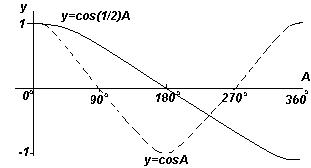
It is, we use the sin (X + π / 2) cos x formula \u003d cos x. This formula can be understood as follows: The function y \u003d COS X takes the same values \u200b\u200bas the function y \u003d sin x, but by π / 2 before. For example, the function y \u003d SIN X takes a value of 1 at x \u003d π / 2, and the function y \u003d cos x \u003d sin (x + π / 2) takes the same value at x \u003d 0. This means the following: for each The scarf points y \u003d sin x is the point of the graph y \u003d COS X, in which the ordinate is the same, and the abscissa is π / 2 less (Fig. 11.5). Therefore, the Y \u003d COS X graph will succeed, if you move the graph y \u003d sin x along the abscissa axis per π / 2 to the left. In fig.11.5, the graph of the function y \u003d COS X is depicted with a solid curve.

So, we found out that the cosine schedule is converted

sinus graphics (shift) from the sinus graph. Cases when a schedule of one function can be obtained by conversion from the graphics of another function, are interesting in themselves, so let's say about them a few words.

How, for example, will the function of the Y \u003d 2 SIN X function look like? It is clear that the ordinates of the points of this graph are obtained from the ordinates of the respective points of the y \u003d SIN x multiplication by 2, so that our schedule is depicted with a solid curve in Fig. 11.6. It can be said that the graph Y \u003d 2 SIN X is obtained from the graph y \u003d sin x with a stretching twice along the ordinate axis.

Fig. 11.7. y \u003d sin 2x.

Now we construct the graph of the function y \u003d sin 2x. Easy to understand

Fig. 11.8. y \u003d sin (2x + π / 3).

that the function y \u003d sin 2x takes the same meaning as the function y \u003d sin x, but with two times smaller values \u200b\u200bof x. For example, the function y \u003d SIN X takes a value of 1 at x \u003d π / 2, and the function y \u003d sin 2x is already at x \u003d π / 4; In other words, to obtain a graph y \u003d sin 2x, it is necessary to reduce the abscissa of all points of the scratch y \u003d SIN x twice, and the orders left unchanged. What is obtained is shown in Fig. 11.7. It can be said that the graph y \u003d sin 2x (the solid line in Fig.11.7) is obtained from the image y \u003d sin x compression 2 times to the axis of the ordinate.

Let's try to still build a graph of the function y \u003d sin (2x + π / 3). It is clear that it should be obtained by some conversion from the graph y \u003d sin 2x. At first glance, it may seem that this conversion is shifting to the left by π / 3 along the abscissa axis, by analogy with what is shown in Fig.11.5. However, if it were so, it would have happened, for example, that the function y \u003d sin (2x + π / 3) takes the value 1 at x \u003d π / 4 - π / 3 \u003d π / 12, which is not true (check !). Correct this: sin (2x + π / 3) \u003d sin 2 (x + π / 6), so that the function y \u003d sin (2x + π / 3) takes the same meanings as the function y \u003d sin 2x, but π / 6 before. So the shift to the left is not π / 3, and on π / 6 (Fig.11.8).

Curves that are graphs of functions Y \u003d A SIN BX, where a 6 \u003d 0, b 6 \u003d 0 is called sinusoids. Note that the crooked "cosineida" is not necessary: \u200b\u200bas we have seen, the cosine schedule is the same curve as the sinus schedule, only otherwise

naya relative to the coordinate axes.

Task 11.2. What are the coordinates of the points marked in fig. 11.8 question marks?

Task 11.3. Take a candle, a thin sheet of paper and a sharp knife. Mix the sheet of paper on the candle in a few layers and gently cut this candle together with the paper by the scraching knife. Now expand the paper. You will see that it turned out to be cut along the wavy line. Prove that this wavy line is a sinusoid.

Comment. If you build graphs of trigonometric functions on the checkered paper, it is convenient to choose a slightly different scale along the axes so that the integer number of cells corresponded to the abscissum axis. For example, this scale is often chosen: along the axis, the ordinate segment 1 takes two cells, along the abscissa axis, the length of the length π takes 6 cells.

Task 11.5. Build features:

a) y \u003d arcsin x; b) y \u003d arccos x.

Let's see how the solutions of equations sin x \u003d a and cos x \u003d a look like on the charts. These solutions are the abscissions of the intersection points of the horizontal direct Y \u003d A with the graph of the functions y \u003d sin x (respectively y \u003d cos x). In fig. 11.9, 11.10 Two series of solutions obtained at -1 are clearly visible.< a < 1.

According to the graphics of sinus and cosine, it can be seen at what periods these functions increase, and in some decrease. It is clear, for example, that the function y \u003d SIN X increases on segments [-π / 2; π / 2],

If you know what the graphics of the simplest look elementary functions, Or you know how to quickly build them at characteristic points, you will also be able to quickly build on their basis the graphics of more complex functions of the same class. To do this, there are rules for converting graphs of functions. They are easily remembered, but if you are still not sure as a result, check it on one or two good points. These rules, of course, are common to all functions, and not just for those who study at school, so the famous schedule will then be called specified.

Let the function schedule set y. = f.(x.) . To build a schedule function

1. y. = mF.(x.) where m. \u003e 0 I. m. ≠ 1, you need the ordinates of the specified graph points to multiply on m.. Such a transformation is called stretching from axis x. C coefficient m., if a m. > 1, and compression to the axis x.if 0< m. < 1.
2. y. = -F.(x.) f.(x.) transformation of symmetry Regarding axis x.. (Symmetry transformation - mirror reflection relatively straight.)
3. y. = f.(x.) + n. , it turns out from the schedule of the function f.(x.) parallel transfer The latter along the ordinate axis on n. units up if n. \u003e 0 and, respectively, on | n.| units down if n.
4. y. = f.(kX.) where k. \u003e 0 I. k. ≠ 1. The desired graph of the function is obtained from the specified compression with coefficient k. to the axis y. (if 0< k. < 1 указанное "сжатие" фактически является stretching With a 1 / coefficient k.)
5. y. = f.(−x.) It turns out from the function schedule f.(x.) transformation of symmetry Regarding axis y.
6. y. = f.(x + L.) It turns out from the function schedule f.(x.) parallel transfer Last on l. units left if l. \u003e 0 and, respectively, on | l.| units to the right if m. < 0.

For example, let the function schedule set y. = √x._ .

To build graphs of other features containing an argument ( x.) Under the sign square root, We use the rules listed above. A specified schedule repeat in the newly drawn "pencil pale" axes, the required schedule, which will work out after transformations, make more intense. In the notebook, you can remove unnecessary by the eraser, only the result of the task will remain.

Note that the parallel chart transfer relative to one of the axes in any side is equivalent to the transfer of this axis relative to the graph in the opposite direction. Therefore, the 3rd and 6th rules can be combined as follows: To build a graph of the function
y. = f.(x. − m.) + n.
need to perform parallel transfer of the entire plane of the coordinate so that the beginning new system Coordinates x." y." There was a point O." (m.;n.). Obviously, instead of redrawing a chart twice, it's easier to turn the axis.

y. = √x._ . Build a chart function y. = √x. + 3____ − 1.

In this case m. = −3, n. \u003d -1. If there are difficulties in identifying signs m. and n., then write a function formula so that it coincides with the rule

y. = f.(x. − m.) + n. ; y. = √x. − m._____ + n. ; y. = √x. − (−3)_______ + (−1)

Construction perform so. Blacks of Axis necessary system coordinates. We find a point with coordinates (-3; -1). We carry out the "pale pencil" straight parallel to the main axes through it. This is an auxiliary coordinate system. In this (pencil) system of coordinates, we build a schedule y. = √x._ . Relative to the main coordinate system, it is a schedule of function y. = √x. + 3____ − 1. Those., If the pencil is removed by the eraser, then the schedule will remain, which was required to build.

If you need to combine only parallel transfers to build a function schedule, it is still in what order to perform them, and it's noted that to transfer - axis or curves. But if you need to build a chart of a complex function, using and transferring, and stretching compression, and reflections, then the procedure for performing operations should be carefully followed.

Conversion sequence when building graphs.

Let the function schedule set y. = f.(x.) and you need to build a graph of the function y. = m · F.(kX. + l.) + n. where k, l, m, n - Numbers.

1. Write a function formula in the form y. = m · F.(k · (x + l./ k.)) . we take out the brackets coefficient when h. In the argument function.
2. We produce compression with the coefficient k. Along the axis Oh to the axis Oy.. (If a k. Oy.)
3. If a k. Oy.
4. l./ k. units left or right (depending on the sign for a positive number left).
5. We produce stretching with the coefficient m. from axis Oh. (along the axis OY.). (If a m. OX.)
6. If a m. OX.
7. We carry out a parallel transfer (shift) of the resulting schedule on n. units up or down (depending on the sign, with n. \u003e 0 up).

Example 8. Set function schedule y. = √x._ . Build a chart function y. = −0,5√3x. − 12______ + 2.

1. Record the function formula in the form y. \u003d -0,5 · √3 · ( x. − 4)_______ + 2 ,
those. we take out the brackets coefficient when h. Under the sign of a square root, taking into account the fact that 12/3 \u003d 4.
2. Build a well-known function schedule. -
3. We produce compression 3 times to the axis Oy.. ——

4. - (symmetry transformation relative to the axis Oy. Not required, because k. = 3 > 0).
5. We shift the resulting schedule for 4 units to the right. -
6. We produce compression 2 times (stretching with a coefficient of 0.5) to the axis Oh.. ——
7. Symmetrically reflect the schedule regarding the axis OX.. ——
8. We shift the last to 2 units up. Received the required schedule. -

Check the result by "convenient" points. For example, x. 1 \u003d 4 and x. 2 = 16.
y. 1 \u003d -0.5√3 · 4 - 12 _____ + 2 = 2.
y. 2 \u003d -0.5√3 · 16 - 12 _____ + 2 = −1.
Points with coordinates (4; 2) and (16; -1) really belong to the latest graphics.

From the graphs it is clear that:

1. Sinus and cosine graphs oscillate in the range between -1 and 1
2. The cosine curve has the same form as the sinus curve, but shifted relative to it by 90 o
3. The sinus and cosine curves are continuous and repeated with a period of 360 o, the tangent curve has breaks and repeats with a period of 180 o.

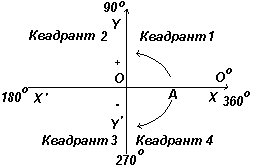In fig. Left show perpendicular axes XX "and YY"; Crossing at the beginning of the coordinates of O. When working with measurement schedules to the right and upwards are considered positive, left and down from O - negative. Let OA freely rotates relative to O. When turning OA counterclockwise, the measured angle is considered positive, and when turning clockwise is negative.

Schedule. Positive or negative
Direction when driving around the circle.

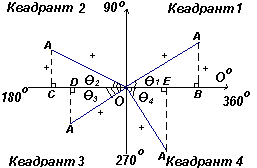Let OA rotates counterclockwise in such a way that θ 1 is any angle in the first quadrant, and we will construct a perpendicular AB to obtain a rectangular triangle of the OAV in Fig. left. Since all three sides of the triangle are positive, trigonometric functions of sinus, cosine and tangent in the first quadrant will be positive. (Note that the OA length is always positive because it is a radius of a circle.)
Let OA rotates further in such a way that θ 2 is any angle in the second quadrant, and build speakers so that it formed right triangle OAS. Then sin θ 2 \u003d + / + \u003d +; cos θ 2 \u003d + / - \u003d -; TG θ 2 \u003d + / - \u003d -. Let the OA rotates further in such a way that θ 3 is any angle in the third quadrant, and we construct an AD so that a rectangular triangle of the OAD formed. Then sin θ 3 \u003d - / + \u003d -; cos θ 3 \u003d - / + \u003d -; TG θ 3 \u003d - / - \u003d +.

Schedule. Treatment of corners B.
Different quadrants.

Let OA rotates further in such a way that θ 4 is any angle in the fourth quadrant, and build ae so that a rectangular triangle OAU is formed. Then sin θ 4 \u003d - / + \u003d -; cos θ 4 \u003d + / + \u003d +; TG θ 4 \u003d - / + \u003d -.

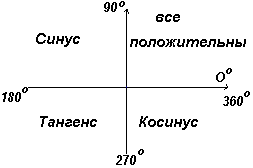
In the first quadrant, all trigonometric functions have positive values, in the second only sinus is positive, in the third - only tangent, in the fourth only cosine, which is shown in Fig. left.

Knowledge of angles of an arbitrary value is necessary when finding, for example, all angles between 0 o and 360 o, the sinus of which is equal to, say, 0.3261. If you enter into a calculator 0,3261 and press the SIN -1 button, we will receive the answer of 19.03 o. However, there is a second angle between 0 o and 360 o, which does not show the calculator. Sinus is also positive in the second quadrant. Another angle is shown in Fig. lower as an angle θ, where θ \u003d 180 o is 19.03 o \u003d 160.97 o. Thus, 19.03 o and 160.97 o are the angles in the range from 0 o to 360 o, the sinus of which is 0.3261.

Be careful! The calculator gives only one of these values. The second value should be determined according to the theory of angles of an arbitrary value.

Example 1.

Find all the corners in the range from 0 o to 360 o, the sinus of which is -0,7071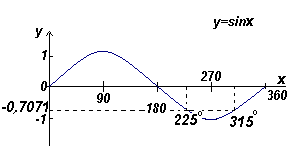

Decision:
The angles whose sine is equal to -0,7071 o are in the third and fourth quadrant, since the sinus is negative in these quadrants (see fig. Left).

Schedule. Finding all angles by
specified sinus value (example)

From the following pattern θ \u003d arcsin 0,7071 \u003d 45 o. Two angle in the range from 0 o to 360 o, the sinus of which is -0.7071, it is 180 o +45 o \u003d 225 o and 360 o - 45 O \u003d 315 o.

Note. Calculator gives only one answer.
Schedule. Finding all angles by
specified sinus value (example)

Example 2.

Find all the angles between 0 o and 360 o, the tangent of which is 1, 327.

Decision:
Tangent is positive in the first and third quadrants - rice. left.
Schedule. Finding all angles by

From rice below θ \u003d arctg1,327 \u003d 53 o.
Two angle in the range of 0 o to 360 o, the tangent of which is 1.327, it is 53 o and 180 o + 53 O, i.e. 233 o.
Schedule. Finding all angles by
The specified value of Tangent (example)

Let OR in fig. To the left is the vector of a single length, freely rotating counterclockwise around O. in one turn turns around the circle shown in Fig. and divided by sectors of 15 o. Each radius has a horizontal and vertical component. For example, for 30 o, the vertical component is TS, and horizontal - oS.

From the definition of trigonometric functions
sIN30 O \u003d TS / TO \u003d TS / 1, i.e. TS \u003d SIN30 O and cOS30 O \u003d OS / TO \u003d OS / 1, i.e. OS \u003d COS30 O

The vertical component TS can be transferred to the graph in the form T "S", which is equal to the value corresponding to the angle of 30 o on the graph Y dependence on the angle of the corner. If all vertical components, like TS, transfer to the schedule, then the sinusoid is shown in Fig. above.

If all horizontal components, similar OS, are proposed to a graph of dependence in the angle of the corner, will turn out to be a cosine. These projections are easy to visualize, redrawing a circle with the OR radius and the beginning of the reference of the corners from the vertical, as shown in the figure on the left.
From fig. It can be seen that the sinusoid has the same form as the cosine one, but shifted by 90 o.

Periodic functions and period
Each of the graphs of functions shown in four rice. above, repeated with an increase in the angle A, so they are called periodic functions.
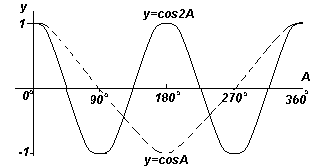
Functions y \u003d sina and y \u003d cosa are repeated every 360 o (or 2π radians), therefore 360 \u200b\u200bo is called Period These functions. The functions y \u003d sin2a and y \u003d cos2a are repeated every 180 o (or π radians), therefore 180 o is the period for these functions.
In general, if Y \u003d SINPA and Y \u003d COSPA (where p is a constant), then the function period is 360 o / p (or 2π / p radians). Therefore, if y \u003d sin3a, then the period of this function is 360 o / 3 \u003d 120 o, if y \u003d cos4a, then the period of this function is 360 o / 4 \u003d 90 o.

Amplitude
Amplitude called maximum value sinusoids. Each of the graphs 1-4 has amplitude +1 (i.e. they oscillate between +1 and -1). However, if Y \u003d 4Sina, each of the values \u200b\u200bof SINA is multiplied by 4, thus, the maximum amount of amplitude is 4. Similarly, the amplitude for Y \u003d 5COS2a is equal to 5, and the period is 360 o / 2 \u003d 180 o.

Example 3.
Construct y \u003d 3sin2a in the range from a \u003d 0 o to a \u003d 360 o.

Decision:
Amplitude \u003d 3, period \u003d 360 o / 2 \u003d 180 o.

Example 4.
Build a graph Y \u003d 4COS2X in the range from x \u003d 0 o to x \u003d 360 o

Decision:
Amplitude \u003d 4. period \u003d 360 O / 2 \u003d 180 O.

Angles of delay and advance
The curves of the sinus and cosine are not always starting at 0 o. To take into account this circumstance, the periodic function is represented as y \u003d sin (a ± α), where α is the phase shift relative to Y \u003d SINA and Y \u003d COSA.

By drawing up a table of values, you can construct a graph of the function y \u003d sin (A-60 O) shown in Fig. left. If the y \u003d SINA curve begins in 0 o, then the curve y \u003d sin (A-60 O) begins in 60 o (i.e. its zero value is 60 o the right). Thus, they say that y \u003d sin (A-60 O) delays Regarding Y \u003d SINA by 60 o.
Schedule. y \u003d sin (A-60 O) (sinusoid).

By drawing up a table of values, you can construct a graph of the function Y \u003d COS (A + 45 O) shown in Fig. below.
If the y \u003d cosa curve begins in 0 o, then the y \u003d cos curve (A + 45 O) begins on 45 o left (i.e. its zero value is 45 ° before).
Thus, they say that the graph Y \u003d COS (A + 45 O) ahead Graph y \u003d cosa 45 o.
Schedule. Y \u003d COS (A + 45 O) (cosineida).

IN general, the graph y \u003d sin (A-α) delays relatively y \u003d sina angle α.
The cosineoid has the same form as the sinusoid, but starts to 90 o left, i.e. It is ahead of it for 90 o. Consequently, Cosa \u003d Sin (A + 90 O).

Example 5.
Build a graph Y \u003d 5Sin (A + 30 O) in the range from A \u003d 0 O to A \u003d 360 O

Decision:
Amplitude \u003d 5, period \u003d 360 o / 1 \u003d 360 o.
5Sin (A + 30 O) ahead of 5SINA by 30 o. It starts 30 ° before.
Graph y \u003d 5Sin (A + 30 O) (sinusoid).

Example 6.
Build a graph Y \u003d 7Sin (2a-π / 3) in the range from A \u003d 0 O to A \u003d 360 O.

Decision:
Amplitude \u003d 7, period \u003d 2π / 2 \u003d π radians
In general y \u003d sin (pt-α) is renewed relative to Y \u003d SINPT on α / p, therefore, 7sin (2a-π / 3) delays relative to 7Sin2a on (π / 3) / 2, i.e. on π / 6 radians or 30 o

Sinusoid type asin (ωt ± α). Phase angle. Phase shift.

Let OR in Fig. Left is a vector freely rotating counterclockwise around O with a speed Ω radian / s. Rotating vector is called phase vector. Through Time T Seconds, the OR will turn to the angle ωt radian (in fig. On the left it is the TOR angle). If you are perpendicular to or build st, then sinωt \u003d ST / OT, \u200b\u200bi.e. ST \u003d otsinωt.
If all similar vertical components are proprietary to the dependence of ωt, it turns out a sinusoid with an AM amplitude.

If the phase vector OR makes one turnover (ie 2π radians) for tons, then the angular velocity ω \u003d 2π / t Rad / s, from where
T \u003d 2π / Ω (C), where
T - that period
The number of total periods passing in 1 second is called frequency f.
Frequency \u003d (number of periods) / (second) \u003d 1 / t \u003d ω / 2π Hz, those. f \u003d ω / 2π Hz
Therefore, the angular speed
ω \u003d 2πf Rad / s.

If in general the sinusoidal function looks like y \u003d sin (ωt ± α), then
A - amplitude
Ω - angular speed
2π / Ω - period T, with
Ω / 2π - Frequency F, Hz
α is an angle of ahead or delay (relative to y \u003d asinωt) in radians, it is also called a phase angle.

Example 7.
AC is set as i \u003d 20sin (90πT + 0.26) amps. Determine the amplitude, period, frequency and phase angle (in degrees)

Decision:
i \u003d 20sin (90πt + 0.26) and therefore
the amplitude is equal20 A.
corner speed Ω.\u003d 90π, therefore,
t. period\u003d 2π / ω \u003d 2π / 90π \u003d 0.022 c \u003d 22ms
frequency f. \u003d 1 / t \u003d 1 / 0.022 \u003d 45.46 Hz
phase angle α. \u003d 0.26 Rad. \u003d (0.26 * 180 / π) O \u003d 14.9 O.

Example 8.
The oscillating mechanism has a maximum displacement of 3 m and a frequency of 55 Hz. During t \u003d 0, the displacement is 100 cm. Express the offset in the general form asin (ωt ± α).

Decision
Amplitude \u003d maximum offset \u003d 3m
The angular velocity ω \u003d 2πf \u003d 2π (55) \u003d 110 πrad. / S
Consequently, the offset 3sin (110πt + α) m.
At t \u003d 0 offset \u003d 100cm \u003d 1m.
Consequently, 1 \u003d 3Sin (0 + α), i.e. sinα \u003d 1/3 \u003d 0.33
Therefore, α \u003d arcsin0,33 \u003d 19 o
So, the offset is 3Sin (110 πT + 0.33).

Example 9.
The value of instantaneous strength in the scheme alternating current In any T, seconds are specified as V \u003d 350SIN (40πT-0.542) in. To find:
a) amplitude, period, frequency and phase angle (in degrees)
b) voltage value at t \u003d 0
c) voltage value at t \u003d 10 ms
d) the time for which the voltage will first reach the value of 200 V.
Decision:
a) amplitude is 350 V, the angular velocity is Ω \u003d 40π
Hence,
The period T \u003d 2π / ω \u003d 2π / 40π \u003d 0.05 C \u003d 50ms
Frequency F \u003d 1 / T \u003d 1 / 0.05 \u003d 20 Hz
Phase angle \u003d 0.542 Run (0.542 * 180 / π) \u003d 31 o with delay relative to V \u003d 350SIN (40πT)
b) if T \u003d 0, then v \u003d 350sin (0-0.542) \u003d 350sin (-31 O) \u003d - 180.25 V
c) if t \u003d 10 ms, then v \u003d 350sin (40π10 / 10 3 -0.542) \u003d 350sin (0.714) \u003d 350sin41 o \u003d 229.6 V
d) if V \u003d 200 and, then 200 \u003d 350sin (40πt-0,542) 200/350 \u003d sin (40πT-0,542)

Schedule. Oscillatory mechanism
(example, sinusoid).

v \u003d 350SIN (40πT-0.542) Therefore, (40πT-0.542) \u003d ArcSin200 / 350 \u003d 35 O or 0.611 is glad.
40πt \u003d 0.611 + 0.542 \u003d 1,153.
Consequently, if V \u003d 200V, then T \u003d 1,153 / 40π \u003d 9,179 ms