Calculate by integration by parts. Complex integrals
The method of integration by parts is mainly used when the integrand consists of the product of two factors of a certain type. The formula for integration by parts is:
It makes it possible to reduce the calculation of the given integral 
to the calculation of the integral 
which turns out to be simpler than the given one.
Most of the integrals calculated by the method of integration by parts can be divided into three groups:
1. Integrals of the form 
,
,
where 
- polynomial, 
- a number that is not equal to zero
In this case, through 
denote a polynomial 
.
2. Integrals of the form 
,
,
,
,
where 
Is a polynomial.
In this case, through 
denote 
, and the rest of the integrand through 
:
3. Integrals of the form 
,
where 
- numbers.
In this case, through 
denote 
and apply the formula of integration by parts twice, returning as a result to the original integral, after which the original integral is expressed from equality.
Comment: In some cases, to find a given integral, the integration by parts formula must be applied several times. Also, the method of integration by parts is combined with other methods.
Example 26.
Find the integrals by the method by parts: a) 
; b) 
.
Decision.
b) 
3.1.4. Integration of fractional rational functions
Fractional rational function(rational fraction) is a function equal to the ratio of two polynomials: 
where 
- polynomial of degree 
,
- polynomial of degree
.
The rational fraction is called correctif the degree of the polynomial in the numerator is less than the degree of the polynomial in the denominator, i.e. 
, otherwise (if 
) the rational fraction is called wrong.
Any irregular rational fraction can be represented as the sum of a polynomial 
and the correct rational fraction by dividing the numerator by the denominator according to the rule of dividing polynomials:
,
where 
- whole part from division, 
- correct rational fraction, 
- remainder of the division.
Regular rational fractions of the form:
I. 
;
II. 
;
III. 
;
IV. 
,
where 
,
,
,
,
,
,
- real numbers and 
(i.e. the square trinomial in the denominator of the III and IV fractions has no roots - the discriminant is negative) are called simplest rational fractions I, II, III and IV types.
Integration of elementary fractions
Integrals of the simplest fractions of four types are calculated as follows.
I) 
.
II), 
.
III) To integrate the simplest fraction of type III in the denominator, a full square is allocated, the replacement is made 
... The integral after the substitution is split into two integrals. The first integral is calculated by selecting the derivative of the denominator in the numerator, which gives a tabular integral, and the second integral is transformed to the form 
, as 
, which also gives the tabular integral.
;
IV) To integrate the simplest type IV fraction in the denominator, a full square is allocated, the replacement is made 
... The integral after the substitution is split into two integrals. The first integral is calculated by substitution 
, and the second with the help of recurrence relations.
Example 27.
Find integrals of simplest fractions:
and) 
; b) 
; in) 
.
Decision.
and) 
.
Any regular rational fraction, the denominator of which can be factorized, can be represented as a sum of the simplest fractions. Decomposition into the sum of the simplest fractions is carried out by the method of undefined coefficients. It is as follows:
corresponds to one fraction of the form 
;
- to each denominator multiplier 
corresponds to the amount 
fractions of the form
corresponds to a fraction of the form 
;
- each square factor of the denominator 
corresponds to the amount 
fractions of the form
where are undefined coefficients.
To find undefined coefficients, the right-hand side in the form of the sum of the simplest fractions is brought to a common denominator and transformed. The result is a fraction with the same denominator as on the left side of the equality. Then the denominators are discarded and the numerators equal. The result is an identity equality, in which the left-hand side is a polynomial with known coefficients, and the right-hand side is a polynomial with undefined coefficients.
There are two ways to determine unknown coefficients: the undefined coefficient method and the partial value method.
Undefined coefficient method.
Because polynomials are identically equal, then the coefficients at the same degrees are equal 
... Equating the coefficients at the same degrees 
in the polynomials of the left and right sides, we obtain a system of linear equations. Solving the system, we determine the undefined coefficients.
Private value method.
Because polynomials are identically equal, then, substituting for 
in the left and right parts of any number, we get the correct equality, linear with respect to the unknown coefficients. Substituting so many values 
how many unknown coefficients, we obtain a system of linear equations. Instead 
you can substitute any numbers in the left and right parts, but it is more convenient to substitute the roots of the denominators of fractions.
After finding the values \u200b\u200bof the unknown coefficients, the original fraction is written as a sum of the simplest fractions in the integrand, and the previously considered integration is carried out for each simplest fraction.
Integration scheme rational fractions:
1. If the integrand is incorrect, then it is necessary to represent it as a sum of a polynomial and a regular rational fraction (that is, divide the numerator polynomial by the denominator polynomial with a remainder). If the integrand is correct, go straight to the second point of the scheme.
2. Factor the denominator of the correct rational fraction, if possible.
3. Expand a regular rational fraction into the sum of the simplest rational fractions using the method of undefined coefficients.
4. Integrate the resulting sum of the polynomial and the simplest fractions.
Example 28.
Find integrals of rational fractions:
and) 
; b) 
; in) 
.
Decision.
and) 
.
Because the integrand is an irregular rational fraction, then we select the whole part, i.e. we represent it as a sum of a polynomial and a regular rational fraction. Divide the polynomial in the numerator by the polynomial in the denominator with an angle.
The initial integral will take the form: 
.
Let's expand the regular rational fraction into the sum of the simplest fractions using the method of indefinite coefficients:
, we get:
Solving the system of linear equations, we obtain the values \u200b\u200bof the undefined coefficients: AND = 1; IN = 3.
Then the required decomposition has the form: 
.
=
.
b) 
.
.
Discard the denominators and equate the left and right sides:
Equating the coefficients at the same degrees 
, we get the system:
Solving a system of five linear equations, we find the undefined coefficients:
.
Let us find the initial integral, taking into account the resulting expansion:
.
in) 
.
Let's expand the integrand (regular rational fraction) into the sum of the simplest fractions using the method of undefined coefficients. We look for the decomposition in the form:
.
Reducing to a common denominator, we get:
Discard the denominators and equate the left and right sides:
To find undefined coefficients, we use the method of partial values. Let's add 
particular values \u200b\u200bat which the factors vanish, that is, we substitute these values \u200b\u200binto the last expression and we get three equations:
; 
;
; 
;
; 
.
Then the required decomposition has the form:
Let us find the initial integral, taking into account the resulting expansion:
Examples of integration by parts of a similar composition are given to 1st and 2nd year students. These tasks were given during the test at the L.N. I. Frank. So that the formulas in the problems and answers are not repeated, we will not describe the problems. According to the condition of the tasks, you need to either "Find the integral" or "Calculate the integral".
Example 8. The integral is found by the rule of integration by parts int (u * dv) \u003d u * v-int (v * du). The main thing here is to choose the right functions for the rule. (For yourself, remember that for dv, if possible, choose periodic functions or those that, when differentiated, up to a factor give themselves - an exponent). In this integral, the sine must be introduced under the differential
Further integration is quite simple and we will not dwell on details. 
Example 9. Again, you need to apply the rule of integration by parts u * dv. Here we have the product of a periodic function and an exponent, so it is up to you to choose what is better to enter under the differential. You can use both an exponent and a cosine (in each case we get a recurrent formula). 
Reapply integration by parts 
We came to a recurrent formula. If we write down the integral that we were looking for and the result of the calculations, we get two similar terms
We group them and find the required integral
Example 10. We have a ready-made expression for the integral under the rule u * dv. Find du and integrate 
We reduce the second integral under the tabular formula and calculate it 
Example 11. Let us denote for the new variable cos (ln (x)) \u003d u і we find du, then by introducing under the differential 
We reapply the integration rule to the integral by parts 
Came to a recurring formula
with which we calculate the unknown integral
Example 12. To find the integral, select the full square in the denominator. Further, reducing the denominator to the well-known integration formula, we obtain the arctangent 
Remember the order of the multipliers well. The unit divided by the root of the intercept appears before the arctangent, and this factor is also present in the arctangent before the variable.
Example 13. We are dealing with a similar integral, only in the denominator the quadratic dependence is under the root. Select a complete square and reduce it under the integration formula, which gives the logarithm 
These are the examples on the control or tests. Remember the basic integration schemes well.
If you cannot solve the integral yourself, then ask for help.
Solving integrals is an easy task, but only for a select few. This article is for those who want to learn to understand integrals, but know nothing or almost nothing about them. Integral ... Why is it needed? How to calculate it? What are definite and indefinite integrals? If the only use of an integral you know is to crochet something useful from hard-to-reach places in the shape of an integral icon, then you are welcome! Learn how to solve integrals and why you can't do without it.
We study the concept of "integral"
Integration has been known since ancient Egypt. Of course, not in its modern form, but still. Since then, mathematicians have written many books on this topic. Especially distinguished themselves Newton and Leibniz but the essence of things has not changed. How to understand integrals from scratch? No way! To understand this topic, you still need a basic knowledge of the basics of mathematical analysis. We already have information about, necessary for understanding integrals, in our blog.
Indefinite integral
Suppose we have some kind of function f (x) .
Indefinite integral function f (x) such a function is called F (x) whose derivative is equal to the function f (x) .
In other words, the integral is the reverse derivative or antiderivative. By the way, read about how in our article.
The antiderivative exists for all continuous functions. Also, the sign of a constant is often added to the antiderivative, since the derivatives of functions that differ by a constant coincide. The process of finding the integral is called integration.
Simple example:
In order not to constantly calculate the antiderivatives of elementary functions, it is convenient to put them into a table and use ready-made values:
Definite integral
When dealing with the concept of an integral, we are dealing with infinitesimal quantities. The integral will help to calculate the area of \u200b\u200bthe figure, the mass of an inhomogeneous body, the path traveled with uneven movement, and much more. It should be remembered that the integral is the sum of an infinitely large number of infinitely small terms.
As an example, let's imagine a graph of some function. How to find the area of \u200b\u200ba shape bounded by the graph of a function?
Using the integral! We divide the curvilinear trapezoid, bounded by the coordinate axes and the graph of the function, into infinitely small segments. Thus, the figure will be divided into thin columns. The sum of the areas of the columns will be the area of \u200b\u200bthe trapezoid. But remember that such a calculation will give an approximate result. However, the smaller and narrower the segments, the more accurate the calculation will be. If we reduce them to such an extent that the length tends to zero, then the sum of the areas of the segments will tend to the area of \u200b\u200bthe figure. This is a definite integral, which is written like this:
Points a and b are called the limits of integration.
Bari Alibasov and the "Integral" group By the way! For our readers now there is a 10% discount on
Integral computation rules for dummies
Indefinite integral properties
How to solve an indefinite integral? Here we will look at the properties of the indefinite integral, which will come in handy when solving examples.
- The derivative of the integral is equal to the integrand:
- The constant can be taken out from under the integral sign:
- The integral of the sum is equal to the sum of the integrals. It is also true for the difference:
Definite integral properties
- Linearity:
- The integral sign changes if the integration limits are reversed:
- When any points a, b and from:
We have already found out that the definite integral is the limit of the sum. But how do you get a specific value when solving an example? For this, there is the Newton-Leibniz formula:
Integral solutions examples
Below we will consider several examples of finding indefinite integrals. We offer you to independently understand the intricacies of the solution, and if something is not clear, ask questions in the comments.
To consolidate the material, watch the video on how integrals are solved in practice. Don't be discouraged if the integral isn't given right away. Contact the professional student service and you can handle any triple or curvilinear integral over a closed surface.
The calculator solves integrals with a description of actions in DETAIL in Russian and for free!
Solution of indefinite integrals
It is an online service in one step:
Solution of definite integrals
It is an online service in one step:
- Enter the integrand (integrand function)
- Introduce the lower limit for the integral
- Introduce an upper limit for the integral
Solution of double integrals
- Enter the integrand (integrand function)
Solving Improper Integrals
- Enter the integrand (integrand function)
- Enter the upper region of integration (or + infinity)
- Introduce the lower region of integration (or - infinity)
Solution of triple integrals
- Enter the integrand (integrand function)
- Enter the lower and upper limits for the first region of integration
- Enter the lower and upper limits for the second region of integration
- Introduce the lower and upper limits for the third region of integration
This service allows you to check your calculations for correctness
Opportunities
- Support for all possible mathematical functions: sine, cosine, exponent, tangent, cotangent, square root and cubic, degrees, exponential and others.
- There are examples for input, both for indefinite integrals, and for improper and definite ones.
- Corrects errors in the expressions you entered and offers your own options for input.
- Numerical solution for definite and improper integrals (including for double and triple integrals).
- Support for complex numbers, as well as various parameters (you can specify in the integrand not only the variable of integration, but also other variable parameters)
A definite integral from continuous function f(x) on a finite segment [ a, b] (where) is called the increment of some of its antiderivatives on this segment. (In general, understanding will be noticeably easier if we repeat the topic of the indefinite integral) In this case, the notation is used
As you can see in the graphs below (the increment of the antiderivative function is indicated), definite integral can be either positive or negative (It is calculated as the difference between the value of the antiderivative at the upper limit and its value at the lower limit, i.e., as F(b) - F(a)).
Numbers a and b are called, respectively, the lower and upper limits of integration, and the segment [ a, b] Is a segment of integration.
So if F(x) Is some antiderivative function for f(x), then, according to the definition,
(38)
Equality (38) is called by the Newton-Leibniz formula ... Difference F(b) – F(a) are briefly written as follows:
Therefore, we will write the Newton-Leibniz formula as follows:
(39)
Let us prove that a definite integral does not depend on which antiderivative of the integrand is taken when calculating it. Let be F(x) and Ф ( x) Are arbitrary antiderivatives of the integrand. Since these are antiderivatives of the same function, they differ by a constant term: Ф ( x) = F(x) + C... therefore
Thus, it was established that on the segment [ a, b] increments of all antiderivatives of the function f(x) match.
Thus, to calculate a definite integral, it is necessary to find any antiderivative of the integrand, i.e. the indefinite integral must be found first. Constant FROM is excluded from subsequent calculations. Then the Newton-Leibniz formula is applied: the value of the upper limit is substituted into the antiderivative function b , further - the value of the lower limit a and the difference is calculated F (b) - F (a) . The resulting number will be a definite integral..
When a = b by definition it is accepted
Example 1.
Decision. First, we find the indefinite integral:
Applying the Newton-Leibniz formula to the antiderivative
(at FROM \u003d 0), we get
However, when calculating a definite integral, it is better not to find the antiderivative separately, but to immediately write the integral in the form (39).
Example 2.Calculate definite integral
Decision. Using the formula
Properties of a definite integral
Theorem 2.The value of the definite integral does not depend on the designation of the variable of integration, i.e.
(40)
Let be F(x) Is the antiderivative for f(x). For f(t) the antiderivative is the same function F(t), in which the independent variable is denoted only differently. Hence,
Based on formula (39), the last equality means the equality of the integrals
Theorem 3.A constant factor can be taken out of the sign of a definite integral, i.e.
(41)
Theorem 4.A definite integral of the algebraic sum of a finite number of functions is equal to the algebraic sum of definite integrals of these functions, i.e.
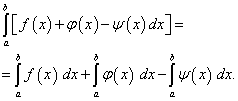(42)
Theorem 5.If the segment of integration is divided into parts, then the definite integral over the entire segment is equal to the sum of definite integrals over its parts, i.e. if a
(43)
Theorem 6.When the limits of integration are rearranged, the absolute value of a definite integral does not change, but only its sign changes, i.e.
(44)
Theorem 7(mean value theorem). The definite integral is equal to the product of the length of the interval of integration by the value of the integrand at some point inside it, i.e.
(45)
Theorem 8.If the upper limit of integration is greater than the lower one and the integrand is nonnegative (positive), then the definite integral is also nonnegative (positive), i.e. if a
Theorem 9.If the upper limit of integration is greater than the lower one and the functions and are continuous, then the inequality
can be integrated term by term, i.e.
(46)
The properties of a definite integral make it possible to simplify the direct calculation of integrals.
Example 5.Calculate definite integral
Using Theorems 4 and 3, and when finding the antiderivatives, the tabular integrals (7) and (6), we obtain
A definite integral with variable upper limit
Let be f(x) Is continuous on the segment [ a, b] function, and F(x) Is its antiderivative. Consider the definite integral
(47)
and after t the variable of integration is indicated in order not to confuse it with the upper limit. When it changes xthe definite integral (47) also changes, i.e. it is a function of the upper limit of integration x, which we denote by F(x), i.e.
(48)
Let us prove that the function F(x) is the antiderivative for f(x) = f(t). Indeed, differentiating F(x), we get
as F(x) Is the antiderivative for f(x), and F(a) Is a constant value.
Function F(x) Is one of the infinite set of antiderivatives for f(x), namely, the one that for x = avanishes. This statement is obtained if in equality (48) we put x = aand use Theorem 1 of the previous section.
Computation of definite integrals by the method of integration by parts and by the method of change of variable
where, by definition, F(x) Is the antiderivative for f(x). If in the integrand we replace the variable
then, in accordance with formula (16), we can write
In this expression
antiderivative function for
Indeed, its derivative, according to the rule for differentiating a complex function , equals
Let α and β be the values \u200b\u200bof the variable t for which the function
takes respectively the values aand b, i.e.
But, according to the Newton-Leibniz formula, the difference F(b) – F(a) there is
