". The first part sets out the provisions that are minimally necessary to understand chemometrics, and the second part - facts that you need to know for a deeper understanding of the methods of multivariate analysis. The presentation is illustrated with examples performed in an Excel workbook Matrix.xls that accompanies this document.

References to examples are placed in the text as Excel objects. These examples are abstract in nature; they are in no way tied to the problems of analytical chemistry. Real examples of the use of matrix algebra in chemometrics are considered in other texts devoted to various chemometric applications.

Most measurements made in analytical chemistry are not direct, but indirect... This means that in the experiment, instead of the value of the desired analyte C (concentration), another value is obtained x (signal) related but not equal to C, i.e. x(C) ≠ C. As a rule, the type of dependence x(C) not known, however, fortunately in analytical chemistry, most measurements are proportional. This means that with an increase in the concentration of C in a times, signal X will increase by the same amount. x(aC) \u003d a x(C). In addition, the signals are also additive, so that the signal from a sample containing two substances with concentrations of C 1 and C 2 will be equal to the sum of signals from each component, i.e. x(C 1 + C 2) \u003d x(C 1) + x(C 2). Proportionality and additivity together give linearity... There are many examples to illustrate the principle of linearity, but it is enough to mention two of the most striking examples - chromatography and spectroscopy. The second characteristic of an experiment in analytical chemistry is multichannel... Modern analytical equipment simultaneously measures signals for many channels. For example, the intensity of light transmission is measured for several wavelengths at once, i.e. range. Therefore, in the experiment we deal with many signals x 1 , x 2 ,...., x n, characterizing the set of concentrations C 1, C 2, ..., C m of substances present in the system under study.

Figure: 1 Spectra

So, an analytical experiment is characterized by linearity and multidimensionality. Therefore, it is convenient to consider experimental data as vectors and matrices and manipulate them using the apparatus of matrix algebra. The fruitfulness of this approach is illustrated by the example shown on, which shows three spectra recorded for 200 wavelengths from 4000 to 4796 cm – 1. The first ( x 1) and the second ( x 2) spectra were obtained for standard samples in which the concentration of two substances A and B is known: in the first sample [A] \u003d 0.5, [B] \u003d 0.1, and in the second sample [A] \u003d 0.2, [B] \u003d 0.6. What can be said about a new, unknown sample, the spectrum of which is designated x 3 ?

Consider three experimental spectra x 1 , x 2 and x 3 as three vectors of dimension 200. By means of linear algebra, one can easily show that x 3 = 0.1 x 1 +0.3 x 2, therefore, the third sample obviously contains only substances A and B at concentrations [A] \u003d 0.5 × 0.1 + 0.2 × 0.3 \u003d 0.11 and [B] \u003d 0.1 × 0.1 + 0.6 × 0.3 \u003d 0.19.

1. Basic information

1.1 Matrices

Matrix called a rectangular table of numbers, for example

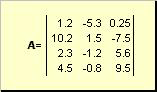
Figure: 2 Matrix

Matrices are designated in bold capital letters ( A), and their elements - with corresponding lowercase letters with indices, i.e. a ij. The first index numbers the rows and the second the columns. In chemometrics, it is customary to denote the maximum value of the index by the same letter as the index itself, but capitalized. Therefore the matrix A can also be written as ( a ij , i = 1,..., I; j = 1,..., J). For the example matrix I = 4, J \u003d 3 and a 23 = −7.5.

Pair of numbers I and J is called the dimension of the matrix and is denoted as I× J... An example of a matrix in chemometrics is the set of spectra obtained for I samples on J wavelengths.

1.2. Basic operations with matrices

Matrices can multiply by numbers... In this case, each element is multiplied by this number. For example -

Figure: 3 Matrix multiplication by number

Two matrices of the same dimension can be elementwise fold and subtract... For example,

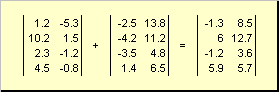
Figure: 4 Matrix addition

As a result of multiplication by a number and addition, a matrix of the same dimension is obtained.

A zero matrix is \u200b\u200ba matrix consisting of zeros. It is designated O... It's obvious that A+O = A, A−A = O and 0 A = O.

The matrix can transpose... During this operation, the matrix is \u200b\u200bflipped, i.e. rows and columns are swapped. Transpose is indicated by a stroke, A"or index A t. So if A = {a ij , i = 1,..., I; j = 1,...,J), then A t \u003d ( a ji , j = 1,...,J; i \u003d 1, ..., I). for example

Figure: 5 Transpose Matrix

It's obvious that ( A t) t \u003d A, (A+B) t \u003d A t + B t.

1.3. Matrix multiplication

Matrices can multiply, but only if they have the appropriate dimensions. Why this is so will be clear from the definition. The product of the matrix A, dimension I× K, and matrices B, dimension K× Jis called the matrix C, dimension I× Jwhose elements are numbers

Thus, to produce AB it is necessary that the number of columns in the left matrix A was equal to the number of rows in the right matrix B... An example of a matrix product -

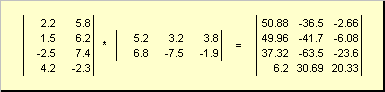
Fig. 6 Matrix product

The matrix multiplication rule can be formulated as follows. To find a matrix element Cstanding at the intersection i-th line and j-th column ( c ij) must be multiplied element by element ith row of the first matrix A on the jth column of the second matrix B and add up all the results. So in the example shown, the element from the third row and the second column is obtained as the sum of the element-wise products of the third row A and the second column B

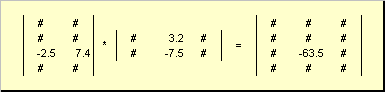
Fig. 7 Matrix product element

The product of matrices depends on the order, i.e. AB ≠ BA, if only for reasons of dimension. It is said to be non-commutative. However, matrix products are associative. It means that ABC = (AB)C = A(BC). In addition, it is also distributive, i.e. A(B+C) = AB+AC... It's obvious that AO = O.

1.4. Square matrices

If the number of columns of the matrix is \u200b\u200bequal to the number of its rows ( I = J \u003d N), then such a matrix is \u200b\u200bcalled square. In this section, we will consider only such matrices. Among these matrices, one can single out matrices with special properties.

Single matrix (denoted I, and sometimes E) is called a matrix in which all elements are equal to zero, except for the diagonal ones, which are equal to 1, i.e.

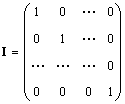
Obviously AI = IA = A.

The matrix is \u200b\u200bcalled diagonalif all its elements, except for the diagonal ones ( a ii) are equal to zero. for example

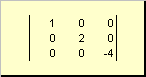
Figure: 8 Diagonal matrix

Matrix A called the top triangularif all its elements below the diagonal are equal to zero, i.e. a ij \u003d 0, for i>j... for example

Figure: 9 Upper triangular matrix

The lower triangular matrix is \u200b\u200bdefined similarly.

Matrix A called symmetrical, if a A t \u003d A... In other words a ij = a ji ... for example

Figure: 10 Symmetric matrix

Matrix A called orthogonal, if a

A t A = AA t \u003d I.

The matrix is \u200b\u200bcalled normal if a

1.5. Trace and determinant

Following square matrix A (denoted by Tr ( A) or Sp ( A)) is the sum of its diagonal elements,

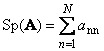
For example,

Figure: 11 Matrix trace

It's obvious that

Sp (α A) \u003d α Sp ( A) and

Sp ( A+B) \u003d Sp ( A) + Sp ( B).

It can be shown that

Sp ( A) \u003d Sp ( A t), Sp ( I) = N,

and also that

Sp ( AB) \u003d Sp ( BA).

Another important characteristic of a square matrix is \u200b\u200bits determinant (denoted by det ( A)). Determination of the determinant in the general case is rather difficult, so we will start with the simplest variant - the matrix A dimension (2 × 2). Then

For a (3 × 3) matrix, the determinant will be

In the case of the matrix ( N× N) the determinant is calculated as the sum of 1 2 3 ... N= N! terms, each of which is equal to

Indexes k 1 , k 2 ,..., k N are defined as all possible ordered permutations r numbers in the set (1, 2, ..., N). Calculation of the determinant of a matrix is \u200b\u200ba complex procedure, which in practice is carried out using special programs. For example,

Figure: 12 Matrix determinant

Note only the obvious properties:

det ( I) \u003d 1, det ( A) \u003d det ( A t),

det ( AB) \u003d det ( A) det ( B).

1.6. Vectors

If the matrix consists of only one column ( J \u003d 1), then such an object is called vector... More precisely, a column vector. for example

One can also consider matrices consisting of one row, for example

This object is also a vector, but row vector... When analyzing data, it is important to understand which vectors we are dealing with - columns or rows. So the spectrum taken for one sample can be considered as a row vector. Then the set of spectral intensities at a certain wavelength for all samples should be treated as a column vector.

The dimension of a vector is the number of its elements.

It is clear that any column vector can be transformed into a row vector by transposition, i.e.

In cases where the form of a vector is not specifically specified, but simply a vector is said, they mean a column vector. We will also adhere to this rule. A vector is denoted by a lowercase straight bold letter. A zero vector is a vector, all elements of which are zero. It is designated 0 .

1.7. Basic operations with vectors

Vectors can be added and multiplied by numbers in the same way as matrices. For example,

Figure: 13 Vector operations

Two vectors x and y are called colinearif there is a number α such that

1.8. Products of vectors

Two vectors of the same dimension N can be multiplied. Let there be two vectors x = (x 1 , x 2 ,...,x N) t and y = (y 1 , y 2 ,..., y N) t. Guided by the rule of multiplication "row by column", we can compose two products from them: x t y and xy t. First piece

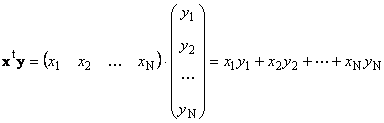
called scalaror internal... Its result is a number. It also uses the notation ( x,y)= x t y... For example,

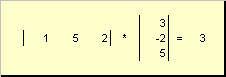
Figure: 14 Inner product (dot product)

Second piece

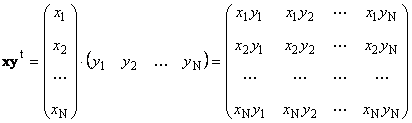
called external... Its result is a matrix of dimension ( N× N). For example,

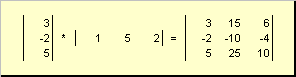
Figure: 15 External work

Vectors, the scalar product of which is equal to zero, are called orthogonal.

1.9. Vector norm

The scalar product of a vector by itself is called a scalar square. This value

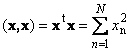
defines a square length vector x... To denote length (also called the norm vector), the notation

For example,

Figure: 16 Vector norm

A vector of unit length (|| x|| \u003d 1) is called normalized. A nonzero vector ( x ≠ 0 ) can be normalized by dividing it by the length, i.e. x = ||x|| (x /||x||) = ||x|| e... Here e = x /||x|| is the normalized vector.

Vectors are called orthonormal if they are all normalized and pairwise orthogonal.

1.10. Angle between vectors

The dot product defines and angle φ between two vectors x and y

If the vectors are orthogonal, then cosφ \u003d 0 and φ \u003d π / 2, and if they are collinear, then cosφ \u003d 1 and φ \u003d 0.

1.11. Vector matrix representation

Each matrix A size I× J can be represented as a set of vectors

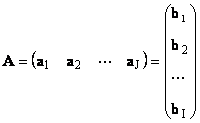
Here each vector a j is an jth column, and the row vector b i is an i-th row of the matrix A

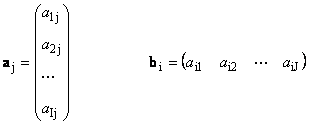
1.12. Linearly Dependent Vectors

Vectors of the same dimension ( N) can be added and multiplied by a number, just like matrices. The result is a vector of the same dimension. Let there be several vectors of the same dimension x 1 , x 2 ,...,x K and the same number of numbers α α 1, α 2, ..., α K ... Vector

y \u003d α 1 x 1 + α 2 x 2 + ... + α K x K

called linear combination vectors x k .

If there are nonzero numbers α k ≠ 0, k = 1,..., K, what y = 0 , then such a set of vectors x k called linearly dependent... Otherwise, the vectors are called linearly independent. For example vectors x 1 \u003d (2, 2) t and x 2 \u003d (−1, −1) t are linearly dependent, since x 1 +2x 2 = 0

1.13. Matrix rank

Consider a set of K vectors x 1 , x 2 ,...,x K dimensions N... The rank of this system of vectors is the maximum number of linearly independent vectors. For example, in the set

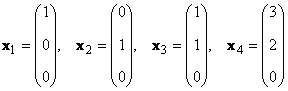
there are only two linearly independent vectors, for example x 1 and x 2, so its rank is 2.

Obviously, if there are more vectors in the set than their dimension ( K>N), then they are necessarily linearly dependent.

By the rank of the matrix(denoted by rank ( A)) is called the rank of the system of vectors of which it consists. Although any matrix can be represented in two ways (column vectors or rows), this does not affect the rank value, since

1.14. inverse matrix

Square matrix A is called nondegenerate if it has a unique reverse matrix A -1 determined by conditions

AA −1 = A −1 A = I.

An inverse matrix does not exist for all matrices. A necessary and sufficient condition for nondegeneracy is

det ( A) ≠ 0 or rank ( A) = N.

Matrix inversion is a complex procedure for which there are special programs. For example,

Figure: 17 Matrix inversion

Let us present formulas for the simplest case - 2 × 2 matrices

If matrices A and B nondegenerate, then

(AB) −1 = B −1 A −1 .

1.15. Pseudoinverse matrix

If the matrix A is degenerate and the inverse matrix does not exist, then in some cases you can use pseudo-inverse a matrix that is defined as such a matrix A + that

AA + A = A.

The pseudo-inverse matrix is \u200b\u200bnot the only one and its type depends on the construction method. For example, for a rectangular matrix, you can use the Moore-Penrose method.

If the number of columns is less than the number of rows, then

A + =(A t A) −1 A t

For example,

Figure: 17a Matrix pseudo-inversion

If the number of columns is greater than the number of rows, then

A + =A t ( AA t) −1

1.16. Vector by matrix multiplication

Vector x can be multiplied by a matrix A suitable dimension. In this case, the column vector is multiplied on the right Axand the row vector is on the left x t A... If the dimension of the vector J, and the dimension of the matrix I× J then the result is a vector of dimension I... For example,

Figure: 18 Vector by matrix multiplication

If the matrix A - square ( I× I), then the vector y = Axhas the same dimension as x... It's obvious that

A(α 1 x 1 + α 2 x 2) \u003d α 1 Ax 1 + α 2 Ax 2 .

Therefore, matrices can be considered as linear transformations of vectors. In particular Ix = x, Ox = 0 .

2. Additional information

2.1. Systems of linear equations

Let be A - matrix size I× J, and b - dimension vector J... Consider the equation

Ax = b

with respect to vector x, dimensions I... In fact, this is a system of I linear equations with J unknown x 1 ,...,x J ... The solution exists if and only if

rank ( A) \u003d rank ( B) = R,

where B is an extended dimension matrix I×( J + 1) consisting of the matrix Apadded with column b, B = (A b). Otherwise, the equations are inconsistent.

If a R = I = J, then the solution is unique

x = A −1 b.

If a R < I, then there are many different solutions that can be expressed through the linear combination J−R vectors. System of homogeneous equations Ax = 0 square matrix A (N× N) has a nontrivial solution ( x ≠ 0 ) if and only if det ( A) \u003d 0. If R \u003d rank ( A)<Nthen exist N−R linearly independent solutions.

2.2. Bilinear and quadratic forms

If a Ais a square matrix, and x and y are vectors of the corresponding dimension, then the scalar product of the form x t Ay called bilinearthe form defined by the matrix A... When x = y expression x t Ax called quadratic form.

2.3. Positive definite matrices

Square matrix Acalled positively definedif for any nonzero vector x ≠ 0 ,

x t Ax > 0.

Similarly defined negatively (x t Ax < 0), non-negative (x t Ax ≥ 0) and not positive (x t Ax ≤ 0) certain matrices.

2.4. Cholesky decomposition

If a symmetric matrix A is positive definite, then there is a unique triangular matrix U with positive elements, for which

A = U t U.

For example,

Figure: 19 Cholesky decomposition

2.5. Polar decomposition

Let be A is a nondegenerate square matrix of dimension N× N... Then there is a unique polar representation

A = SR,

where S is a nonnegative symmetric matrix, and R is an orthogonal matrix. Matrices S and R can be defined explicitly:

S 2 = AA t or S = (AA t) ½ and R = S −1 A = (AA t) −1 A.

For example,

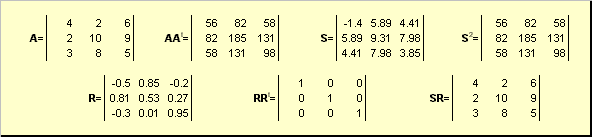
Figure: 20 Polar decomposition

If the matrix A is degenerate, then the expansion is not unique, namely: S still alone, but R maybe a lot. Polar decomposition represents the matrix A as a combination of compression / extension S and turning R.

2.6. Eigenvectors and eigenvalues

Let be A is a square matrix. Vector v called own vector matrices A, if a

Av = λ v,

where the number λ is called own meaning matrices A... Thus, the transformation that the matrix performs A over vector v, is reduced to simple stretching or compression with a coefficient λ. The eigenvector is determined up to multiplication by the constant α ≠ 0, i.e. if a v is an eigenvector, then α v is also an own vector.

2.7. Eigenvalues

Matrix A , dimension ( N× N) cannot be more than N eigenvalues. They satisfy characteristic equation

det ( A − λ I) = 0,

which is an algebraic equation Nth order. In particular, for a 2 × 2 matrix, the characteristic equation has the form

For example,

Figure: 21 Eigenvalues

The set of eigenvalues \u200b\u200bλ 1, ..., λ N matrices A called spectrum A.

The spectrum has a variety of properties. In particular

det ( A) \u003d λ 1 × ... × λ N, Sp ( A) \u003d λ 1 + ... + λ N.

The eigenvalues \u200b\u200bof an arbitrary matrix can be complex numbers, but if the matrix is \u200b\u200bsymmetric ( A t \u003d A), then its eigenvalues \u200b\u200bare real.

2.8. Own vectors

Matrix A, dimension ( N× N) cannot be more than N eigenvectors, each of which corresponds to its own value. To determine the eigenvector v n you need to solve a system of homogeneous equations

(A − λ n I) v n = 0 .

It has a nontrivial solution, since det ( A -λ n I) = 0.

For example,

Figure: 22 Eigenvectors

The eigenvectors of a symmetric matrix are orthogonal.

Eigenvalues \u200b\u200b(numbers) and eigenvectors.
Solution examples

Be yourself

It follows from both equations that.

Let's put, then: .

As a result: Is the second eigenvector.

Let's repeat the important points of the solution:

- the resulting system certainly has a general solution (equations are linearly dependent);

- we select the “game” so that it is whole and the first “x” coordinate is whole, positive and as small as possible.

- check that the particular solution satisfies each equation of the system.

Answer .

There were quite enough intermediate “control points”, therefore, equality checking, in principle, is an unnecessary matter.

In various sources of information, the coordinates of eigenvectors are often written not in columns, but in rows, for example: (and, to be honest, I'm used to writing them in lines myself)... This option is acceptable, but in light of the topic linear transformations technically more convenient to use column vectors.

Perhaps the solution seemed very long to you, but that's only because I commented in great detail on the first example.

Example 2

Matrices

We train ourselves! An approximate example of finishing the task at the end of the lesson.

Sometimes an additional task is required, namely:

write the canonical matrix decomposition

What it is?

If the eigenvectors of the matrix form basis, then it can be represented as:

Where is the matrix composed of the coordinates of the eigenvectors, - diagonal matrix with corresponding eigenvalues.

Such a matrix decomposition is called canonical or diagonal.

Consider the matrix of the first example. Its own vectors linearly independent (non-collinear) and form a basis. Let's compose a matrix from their coordinates:

On the main diagonal matrices in the appropriate order eigenvalues \u200b\u200bare located, and the remaining elements are equal to zero:
- once again I emphasize the importance of the order: "two" corresponds to the 1st vector and therefore is located in the 1st column, "three" - to the 2nd vector.

According to the usual algorithm of finding inverse matrix or gauss-Jordan methodfind ... No, this is not a typo! - before you is a rare event, like a solar eclipse, when the inverse coincided with the original matrix.

It remains to write down the canonical decomposition of the matrix:

The system can be solved with the help of elementary transformations and in the following examples we will use this method. But here the "school" method works much faster. From the 3rd equation we will express: - we will substitute in the second equation:

Since the first coordinate is zero, we obtain a system, from each equation of which it follows that.

And again pay attention to the obligatory presence of linear dependence... If you get only a trivial solution , then either the eigenvalue was found incorrectly, or the system was compiled / solved with an error.

Compact coordinates gives meaning

Eigenvector:

And once again - we check that the found solution satisfies each equation of the system... In the following paragraphs and in subsequent tasks, I recommend that you take this wish as a mandatory rule.

2) For the eigenvalue, according to the same principle, we obtain the following system:

From the 2nd equation of the system, we express: - substitute in the third equation:

Since the "zeta" coordinate is zero, we get a system, from each equation of which a linear dependence follows.

Let be

We check that the solution satisfies every equation in the system.

Thus, the eigenvector:.

3) And finally, the system corresponds to the eigenvalue:

The second equation looks the simplest, so we express from it and substitute it into the 1st and 3rd equations:

Everything is good - a linear relationship has emerged, which we substitute into the expression:

As a result, "x" and "igrek" were expressed through "z":. In practice, it is not necessary to achieve just such relationships, in some cases it is more convenient to express both through or and through. Or even a "train" - for example, "X" through "igrek", and "igrek" through "z"

Let's put, then:

We check that the found solution satisfies each equation of the system and write down the third eigenvector

Answer: eigenvectors:

Geometrically, these vectors define three different spatial directions ("There and back again")by which linear transformation transforms nonzero vectors (eigenvectors) into vectors collinear to them.

If the condition required to find a canonical decomposition, then this is possible here, since different eigenvalues \u200b\u200bcorrespond to different linearly independent eigenvectors. Composing the matrix from their coordinates, the diagonal matrix of the respective eigenvalues \u200b\u200band find inverse matrix .

If, by condition, you need to write matrix of linear transformation in the basis of eigenvectors, then we give the answer in the form. There is a difference, and the difference is significant! For this matrix is \u200b\u200bthe “de” matrix.

Problem with simpler calculations for an independent solution:

Example 5

Find the eigenvectors of a linear transformation given by a matrix

When finding the eigenvalues, try not to bring the matter to the 3rd degree polynomial. In addition, your system solutions may differ from my solutions - there is no unambiguity here; and the vectors you find may differ from the sample vectors up to the proportionality of their respective coordinates. For example, and. It is more aesthetic to present the answer in the form, but it's okay if you stop at the second option. However, there are reasonable limits to everything, the version does not look very good anymore.

An approximate final sample of the assignment at the end of the lesson.

How to solve the problem in the case of multiple eigenvalues?

The general algorithm remains the same, but it has its own peculiarities, and it is advisable to maintain some parts of the solution in a more strict academic style:

Example 6

Find eigenvalues \u200b\u200band eigenvectors

Decision

Of course, we capitalize the fabulous first column:

And, after factoring the square trinomial:

As a result, eigenvalues \u200b\u200bare obtained, two of which are multiples.

Let's find eigenvectors:

1) We will deal with the lonely soldier according to the "simplified" scheme:

From the last two equations, equality is clearly visible, which, obviously, should be substituted into the 1st equation of the system:

There is no better combination:
Eigenvector:

2-3) Now shoot a couple of sentries. In this case, it may turn out either two or one eigenvector. Regardless of the multiplicity of the roots, we substitute the value into the determinant which brings us the following homogeneous system of linear equations:

Eigenvectors are exactly vectors
fundamental decision system

Actually, throughout the entire lesson, we were only engaged in finding the vectors of the fundamental system. Just for the time being, this term was not particularly required. By the way, those clever students who slipped the topic in camouflage coats homogeneous equationswill have to eat it now.

The only action was to remove the extra lines. The result is a one-by-three matrix with a formal "rung" in the middle.
- basic variable, - free variables. There are two free variables, therefore, vectors of the fundamental system are also two.

Let's express the basic variable in terms of free variables:. The zero factor before the "x" allows it to take absolutely any values \u200b\u200b(which is clearly seen from the system of equations).

In the context of this problem, it is more convenient to write the general solution not in a row, but in a column:

The pair has its own vector:
The pair has its own vector:

Note : sophisticated readers can pick up these vectors and orally - just by analyzing the system , but here some knowledge is needed: there are three variables, system matrix rank - unit, which means fundamental decision system consists of 3 - 1 \u003d 2 vectors. However, the vectors found are perfectly visible even without this knowledge, purely on an intuitive level. In this case, the third vector will be written even "more beautifully":. However, I warn you that in another example, simple selection may not be, which is why the disclaimer is intended for experienced people. Besides, why not take, say, as the third vector? After all, its coordinates also satisfy each equation of the system, and the vectors are linearly independent. This option, in principle, is suitable, but "crooked", since the "other" vector is a linear combination of vectors of the fundamental system.

Answer: eigenvalues:, eigenvectors:

A similar example for a stand alone solution:

Example 7

Find eigenvalues \u200b\u200band eigenvectors

A rough example of finishing at the end of the lesson.

It should be noted that in both the 6th and 7th examples, a triple of linearly independent eigenvectors is obtained, and therefore the original matrix is \u200b\u200brepresentable in the canonical decomposition. But such raspberries do not happen in all cases:

Example 8

Decision: compose and solve the characteristic equation:

We open the determinant by the first column:

Further simplifications are carried out according to the considered method, avoiding the 3rd degree polynomial:

- eigenvalues.

Let's find eigenvectors:

1) There are no difficulties with the root:

Do not be surprised, in addition to the kit, variables are also used - there is no difference here.

From the 3rd equation we will express - we will substitute in the 1st and 2nd equations:

From both equations it follows:

Let, then:

2-3) For multiple values, we get the system .

We write down the matrix of the system and, using elementary transformations, bring it to a stepwise form:

With matrix A, if there is a number l such that AX \u003d lX.

Moreover, the number l is called own meaning operator (matrix A) corresponding to vector X.

In other words, an eigenvector is a vector that, under the action of a linear operator, transforms into a collinear vector, i.e. just multiplied by some number. In contrast, improper vectors are more difficult to transform.

Let us write the definition of an eigenvector in the form of a system of equations:

Move all the terms to the left side:

The latter system can be written in matrix form as follows:

(A - lE) X \u003d O

The resulting system always has a zero solution X \u003d O. Such systems in which all free terms are equal to zero are called homogeneous... If the matrix of such a system is square, and its determinant is not equal to zero, then according to Cramer's formulas we always get the only solution - zero. It can be proved that the system has nonzero solutions if and only if the determinant of this matrix is \u200b\u200bequal to zero, i.e.

| A - le | \u003d = 0

This equation with unknown l is called characteristic equation (characteristic polynomial) of the matrix A (linear operator).

It can be proved that the characteristic polynomial of a linear operator does not depend on the choice of the basis.

For example, let us find the eigenvalues \u200b\u200band eigenvectors of the linear operator given by the matrix A \u003d.

For this, we compose the characteristic equation | A - lЕ | \u003d \u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; eigenvalues \u200b\u200bl 1 \u003d (2 - 12) / 2 \u003d -5; l 2 \u003d (2 + 12) / 2 \u003d 7.

To find the eigenvectors, we solve two systems of equations

(A + 5E) X \u003d O

(A - 7E) X \u003d O

For the first of them, the expanded matrix takes the form

,

whence x 2 \u003d c, x 1 + (2/3) c \u003d 0; x 1 \u003d - (2/3) s, i.e. X (1) \u003d (- (2/3) s; s).

For the second of them, the expanded matrix takes the form

,

whence x 2 \u003d c 1, x 1 - (2/3) c 1 \u003d 0; x 1 \u003d (2/3) s 1, i.e. X (2) \u003d ((2/3) s 1; s 1).

Thus, the eigenvectors of this linear operator are all vectors of the form (- (2/3) с; с) with an eigenvalue (-5) and all vectors of the form ((2/3) с 1; с 1) with an eigenvalue 7 ...

It can be proved that the matrix of the operator A in the basis consisting of its eigenvectors is diagonal and has the form:

,

where l i are the eigenvalues \u200b\u200bof this matrix.

The converse is also true: if the matrix A in some basis is diagonal, then all vectors of this basis will be eigenvectors of this matrix.

It is also possible to prove that if a linear operator has n pairwise different eigenvalues, then the corresponding eigenvectors are linearly independent, and the matrix of this operator in the corresponding basis has a diagonal form.

Let us explain this with the previous example. Take arbitrary nonzero values \u200b\u200bof с and с 1, but such that the vectors X (1) and X (2) are linearly independent, i.e. would form the basis. For example, let c \u003d c 1 \u003d 3, then X (1) \u003d (-2; 3), X (2) \u003d (2; 3).

Let us verify the linear independence of these vectors:

12 ≠ 0. In this new basis, the matrix A will take the form A * \u003d.

To verify this, we use the formula A * \u003d C -1 AC. First, find С -1.

С -1 \u003d ;

Quadratic forms

Quadratic form f (x 1, x 2, x n) of n variables is called the sum, each term of which is either the square of one of the variables, or the product of two different variables, taken with a certain coefficient: f (x 1, x 2, x n) \u003d (a ij \u003d a ji).

The matrix A composed of these coefficients is called matrixquadratic form. It's always symmetric matrix (i.e. a matrix symmetric about the main diagonal, a ij \u003d a ji).

In matrix notation, the quadratic form is f (X) \u003d X T AX, where

Indeed

For example, let us write the quadratic form in matrix form.

To do this, we find a matrix of quadratic form. Its diagonal elements are equal to the coefficients of the squares of the variables, and the remaining elements are equal to half of the corresponding coefficients of the quadratic form. therefore

Let the matrix-column of variables X be obtained by a non-degenerate linear transformation of the matrix-column Y, i.e. X \u003d CY, where С is a nondegenerate matrix of order n. Then the quadratic form f (X) \u003d X T AX \u003d (CY) T A (CY) \u003d (Y T C T) A (CY) \u003d Y T (C T AC) Y.

Thus, with a non-degenerate linear transformation C, the matrix of the quadratic form takes the form: A * \u003d C T AC.

For example, let us find the quadratic form f (y 1, y 2) obtained from the quadratic form f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 by a linear transformation.

The quadratic form is called canonical (It has canonical view) if all its coefficients a ij \u003d 0 for i ≠ j, that is,
f (x 1, x 2, x n) \u003d a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 \u003d.

Its matrix is \u200b\u200bdiagonal.

Theorem (no proof is given here). Any quadratic form can be reduced to canonical form using a non-degenerate linear transformation.

For example, we bring to canonical form the quadratic form
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

To do this, first select a complete square with a variable x 1:

f (x 1, x 2, x 3) \u003d 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2) 2 - 5x 2 2 - x 2 x 3.

Now we select a complete square with a variable x 2:

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2) + (5/100) x 3 2 \u003d
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

Then the non-degenerate linear transformation y 1 \u003d x 1 + x 2, y 2 \u003d x 2 + (1/10) x 3 and y 3 \u003d x 3 reduces this quadratic form to the canonical form f (y 1, y 2, y 3) \u003d 2y 1 2 - 5y 2 2 + (1/20) y 3 2.

Note that the canonical form of a quadratic form is not uniquely determined (the same quadratic form can be reduced to canonical form in different ways). However, the canonical forms obtained in various ways have a number of common properties. In particular, the number of terms with positive (negative) coefficients of the quadratic form does not depend on the method of reducing the form to this form (for example, in the example considered, there will always be two negative and one positive coefficient). This property is called the law of inertia of quadratic forms.

Let us verify this by reducing the same quadratic form to its canonical form in a different way. Let's start the transformation with variable x 2:

f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3 (x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 \u003d
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \u003d f (y 1, y 2, y 3) \u003d -3y 1 2 -
+ 3y 2 2 + 2y 3 2, where y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 \u003d (2/3) x 1 + (1/6) x 3 and y 3 \u003d x 1. Here a negative coefficient -3 for y 1 and two positive coefficients 3 and 2 for y 2 and y 3 (and when using another method, we got a negative coefficient (-5) for y 2 and two positive ones: 2 for y 1 and 1/20 for y 3).

It should also be noted that the rank of the matrix of the quadratic form, called the rank of the quadratic form, is equal to the number of nonzero coefficients of the canonical form and does not change under linear transformations.

The quadratic form f (X) is called positively (negatively) certainif for all values \u200b\u200bof the variables that are not equal to zero at the same time, it is positive, i.e. f (X)\u003e 0 (negative, i.e.
f (X)< 0).

For example, the quadratic form f 1 (X) \u003d x 1 2 + x 2 2 is positive definite, since is the sum of squares, and the quadratic form f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 is negative definite, since represents it can be represented as f 2 (X) \u003d - (x 1 - x 2) 2.

In most practical situations, it is somewhat more difficult to establish the definiteness of a quadratic form, therefore one of the following theorems is used for this (we will formulate them without proofs).

Theorem... A quadratic form is positive (negative) definite if and only if all eigenvalues \u200b\u200bof its matrix are positive (negative).

Theorem(Sylvester criterion). A quadratic form is positive definite if and only if all major minors of the matrix of this form are positive.

Major (corner) minor The k-th order of the matrix А of the n-th order is called the determinant of the matrix, composed of the first k rows and columns of the matrix А ().

Note that for negative definite quadratic forms, the signs of the major minors alternate, and the first-order minor must be negative.

For example, let us investigate the quadratic form f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 + 3x 2 2 for sign definiteness.

\u003d (2 - l) *
* (3 - l) - 4 \u003d (6 - 2l - 3l + l 2) - 4 \u003d l 2 - 5l + 2 \u003d 0; D \u003d 25 - 8 \u003d 17;
... Therefore, the quadratic form is positive definite.

Method 2. The main minor of the first order of the matrix А D 1 \u003d a 11 \u003d 2\u003e 0. The main minor of the second order D 2 \u003d \u003d 6 - 4 \u003d 2\u003e 0. Therefore, according to Sylvester's criterion, the quadratic form is positive definite.

Let us examine another quadratic form for definiteness of signs, f (x 1, x 2) \u003d -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Method 1. Let's construct a matrix of the quadratic form A \u003d. The characteristic equation will have the form \u003d (-2 - l) *
* (- 3 - l) - 4 \u003d (6 + 2l + 3l + l 2) - 4 \u003d l 2 + 5l + 2 \u003d 0; D \u003d 25 - 8 \u003d 17;
... Therefore, the quadratic form is negative definite.

Method 2. The main minor of the first order of the matrix A D 1 \u003d a 11 \u003d
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 > 0. Therefore, according to Sylvester's criterion, the quadratic form is negative definite (the signs of the major minors alternate, starting with the minus).

And as another example, let us examine the quadratic form f (x 1, x 2) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 for sign definiteness.

Method 1. Let's construct a matrix of the quadratic form A \u003d. The characteristic equation will have the form \u003d (2 - l) *
* (- 3 - l) - 4 \u003d (-6 - 2l + 3l + l 2) - 4 \u003d l 2 + l - 10 \u003d 0; D \u003d 1 + 40 \u003d 41;
.

One of these numbers is negative and the other is positive. The eigenvalue signs are different. Consequently, the quadratic form can be neither negative nor positive definite, i.e. this quadratic form is not sign definite (it can take values \u200b\u200bof any sign).

Method 2. The main minor of the first order of the matrix A D 1 \u003d a 11 \u003d 2\u003e 0. The major minor of the second order D 2 \u003d \u003d -6 - 4 \u003d -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

The diagonal matrices are the simplest. The question arises whether it is possible to find a basis in which the matrix of a linear operator would have a diagonal form. Such a basis exists.
Let a linear space R n and a linear operator A acting in it be given; in this case the operator A takes R n into itself, that is, A: R n → R n.

Definition. A nonzero vector is called an eigenvector of the operator A if the operator A transforms into a vector collinear to it, that is. The number λ is called the eigenvalue or eigenvalue of the operator A, corresponding to the eigenvector.
Let us note some properties of eigenvalues \u200b\u200band eigenvectors.
1. Any linear combination of eigenvectors of the operator A corresponding to the same eigenvalue λ is an eigenvector with the same eigenvalue.
2. Eigenvectors of the operator A with pairwise distinct eigenvalues \u200b\u200bλ 1, λ 2,…, λ m are linearly independent.
3. If the eigenvalues \u200b\u200bλ 1 \u003d λ 2 \u003d λ m \u003d λ, then the eigenvalue λ corresponds to at most m linearly independent eigenvectors.

So, if there are n linearly independent eigenvectors corresponding to different eigenvalues \u200b\u200bλ 1, λ 2,…, λ n, then they are linearly independent, therefore, they can be taken as a basis of the space R n. Let us find the form of the matrix of the linear operator A in the basis of its eigenvectors, for which we act by the operator A on the basis vectors: then .
Thus, the matrix of the linear operator A in the basis of its eigenvectors has a diagonal form, and the eigenvalues \u200b\u200bof the operator A stand on the diagonal.
Is there another basis in which the matrix is \u200b\u200bdiagonal? The answer to this question is given by the following theorem.

Theorem. The matrix of a linear operator A in the basis (i \u003d 1..n) has a diagonal form if and only if all vectors of the basis are eigenvectors of the operator A.

The rule for finding eigenvalues \u200b\u200band eigenvectors

Let a vector , where x 1, x 2, ..., x n are the coordinates of the vector relative to the basis and is the eigenvector of the linear operator A corresponding to the eigenvalue λ, that is. This relationship can be written in matrix form

. (*)

Equation (*) can be considered as an equation for finding, and, that is, we are interested in non-trivial solutions, since the eigenvector cannot be zero. It is known that nontrivial solutions of a homogeneous system of linear equations exist if and only if det (A - λE) \u003d 0. Thus, for λ to be an eigenvalue of the operator A, it is necessary and sufficient that det (A - λE) \u003d 0.
If the equation (*) is written in detail in coordinate form, then we get a system of linear homogeneous equations:

(1)
where is the matrix of the linear operator.

System (1) has a nonzero solution if its determinant D is equal to zero

Received an equation for finding the eigenvalues.
This equation is called the characteristic equation, and its left-hand side is called the characteristic polynomial of the matrix (operator) A. If the characteristic polynomial has no real roots, then the matrix A has no eigenvectors and cannot be reduced to a diagonal form.
Let λ 1, λ 2,…, λ n be real roots of the characteristic equation, and among them there may be multiple roots. Substituting these values \u200b\u200bin turn into system (1), we find the eigenvectors.

Example 12. The linear operator A acts in R 3 according to the law, where x 1, x 2, .., x n are the coordinates of the vector in the basis , , ... Find the eigenvalues \u200b\u200band eigenvectors of this operator.
Decision. We build the matrix of this operator:
.
We compose a system for determining the coordinates of eigenvectors:

We draw up a characteristic equation and solve it:

.
λ 1,2 \u003d -1, λ 3 \u003d 3.
Substituting λ \u003d -1 into the system, we have:
or
As , then there are two dependent variables, and one free variable.
Let x 1 be a free unknown, then We solve this system in any way and find a general solution to this system: The fundamental system of solutions consists of one solution, since n - r \u003d 3 - 2 \u003d 1.
The set of eigenvectors corresponding to the eigenvalue λ \u003d -1 has the form:, where x 1 is any nonzero number. Let us choose one vector from this set, for example, putting x 1 \u003d 1: .
Arguing similarly, we find the eigenvector corresponding to the eigenvalue λ \u003d 3: .
In the space R 3 the basis consists of three linearly independent vectors, but we have received only two linearly independent eigenvectors, from which the basis in R 3 cannot be composed. Therefore, the matrix A of the linear operator cannot be reduced to a diagonal form.

Example 13. Given a matrix .
1. Prove that the vector is an eigenvector of the matrix A. Find the eigenvalue corresponding to this eigenvector.
2. Find a basis in which the matrix A has a diagonal form.
Decision.
1. If, then - eigenvector

.
Vector (1, 8, -1) is an eigenvector. Eigenvalue λ \u003d -1.
The matrix has a diagonal form in a basis consisting of eigenvectors. One of them is famous. Let's find the rest.
We search for eigenvectors from the system:

Characteristic equation: ;
(3 + λ) [- 2 (2-λ) (2 + λ) +3] \u003d 0; (3 + λ) (λ 2 - 1) \u003d 0
λ 1 \u003d -3, λ 2 \u003d 1, λ 3 \u003d -1.
Let us find the eigenvector corresponding to the eigenvalue λ \u003d -3:

The rank of the matrix of this system is equal to two and is equal to the number of unknowns, therefore this system has only a zero solution x 1 \u003d x 3 \u003d 0. x 2 here can be any nonzero, for example, x 2 \u003d 1. Thus, the vector (0 , 1,0) is an eigenvector corresponding to λ \u003d -3. Let's check:
.
If λ \u003d 1, then we obtain the system
The rank of the matrix is \u200b\u200btwo. We delete the last equation.
Let x 3 be a free unknown. Then x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
Setting x 3 \u003d 1, we have (-3, -9,1) - the eigenvector corresponding to the eigenvalue λ \u003d 1. Verification:

.
Since the eigenvalues \u200b\u200bare real and different, the vectors corresponding to them are linearly independent, so they can be taken as a basis in R 3. Thus, in the basis , , matrix A has the form:
.
Not every matrix of a linear operator A: R n → R n can be reduced to diagonal form, since for some linear operators linearly independent eigenvectors can be less than n. However, if the matrix is \u200b\u200bsymmetric, then exactly m linearly independent vectors correspond to the root of the characteristic equation of multiplicity m.

Definition. A symmetric matrix is \u200b\u200ba square matrix in which the elements symmetric about the main diagonal are equal, that is, in which.
Remarks. 1. All eigenvalues \u200b\u200bof a symmetric matrix are real.
2. The eigenvectors of a symmetric matrix corresponding to pairwise different eigenvalues \u200b\u200bare orthogonal.
As one of the many applications of the studied apparatus, let us consider the problem of determining the shape of a second-order curve.

Definition 9.3. Vector x called own vector matrices ANDif there is such a number λ, that equality holds: AND x= λ x, that is, the result of applying to x linear transformation given by the matrix AND, is the multiplication of this vector by the number λ ... The number itself λ called own number matrices AND.

Substituting into formulas (9.3) x` j \u003d λx j, we obtain a system of equations for determining the coordinates of the eigenvector:

. (9.5)

This linear homogeneous system will have a nontrivial solution only if its main determinant is 0 (Cramer's rule). Writing this condition in the form:

we obtain the equation for determining the eigenvalues λ called characteristic equation... It can be briefly presented as follows:

| A - λE | = 0, (9.6)

since its left side contains the determinant of the matrix A-λE... Polynomial with respect to λ | A - λE| called characteristic polynomial matrices A.

Characteristic polynomial properties:

1) The characteristic polynomial of a linear transformation does not depend on the choice of the basis. Evidence. (see (9.4)), but hence, . Thus, it does not depend on the choice of the basis. Hence, and | A-λE| does not change when switching to a new basis.

2) If the matrix AND linear transformation is symmetric (those. and ij \u003d a ji), then all roots of the characteristic equation (9.6) are real numbers.

Properties of eigenvalues \u200b\u200band eigenvectors:

1) If we choose a basis of eigenvectors x 1, x 2, x 3 corresponding to the eigenvalues λ 1, λ 2, λ 3 matrices AND, then in this basis the linear transformation A has a diagonal matrix:

(9.7) The proof of this property follows from the definition of eigenvectors.

2) If the eigenvalues \u200b\u200bof the transformation AND are different, then the corresponding eigenvectors are linearly independent.

3) If the characteristic polynomial of the matrix AND has three different roots, then in some basis the matrix AND has a diagonal form.

Let us find the eigenvalues \u200b\u200band eigenvectors of the matrix Let's compose the characteristic equation: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 \u003d 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Let's find the coordinates of the eigenvectors corresponding to each found value λ. From (9.5) it follows that if x (1) ={x 1, x 2, x 3) Is the eigenvector corresponding λ 1 \u003d -2, then

- a collaborative but undefined system. Its solution can be written as x (1) ={a,0,-a), where a is any number. In particular, if we require that | x (1) |=1, x (1) =

Substituting into the system (9.5) λ 2 \u003d 3, we obtain a system for determining the coordinates of the second eigenvector - x (2) ={y 1, y 2, y 3}:

from where x (2) ={b, -b, b) or, subject to | x (2) |=1, x (2) =

For λ 3 \u003d 6 find the eigenvector x (3) ={z 1, z 2, z 3}:

, x (3) ={c,2c, c) or in the normalized version

x (3) = You can see that x (1) x (2) = ab - ab= 0, x (1) x (3) = ac - ac= 0, x (2) x (3) = bc- 2bc + bc\u003d 0. Thus, the eigenvectors of this matrix are pairwise orthogonal.

Lecture 10.

Quadratic forms and their relationship with symmetric matrices. Properties of eigenvectors and eigenvalues \u200b\u200bof a symmetric matrix. Reducing the quadratic form to the canonical form.

Definition 10.1.Quadratic form real variables x 1, x 2, ..., x n is a polynomial of the second degree with respect to these variables, which does not contain a free term and terms of the first degree.

Examples of quadratic forms:

(n = 2),

(n = 3). (10.1)

Recall the definition of a symmetric matrix given in the last lecture:

Definition 10.2. The square matrix is \u200b\u200bcalled symmetric, if, that is, if the matrix elements are equal, symmetric about the main diagonal.

Properties of eigenvalues \u200b\u200band eigenvectors of a symmetric matrix:

1) All eigenvalues \u200b\u200bof the symmetric matrix are real.

Proof (for n = 2).

Let the matrix AND looks like: ... Let's compose the characteristic equation:

(10.2) Find the discriminant:

Hence, the equation has only real roots.

2) The eigenvectors of the symmetric matrix are orthogonal.

Proof (for n= 2).

The coordinates of the eigenvectors and must satisfy the equations.