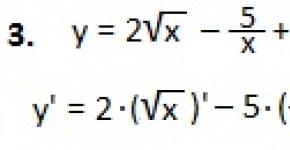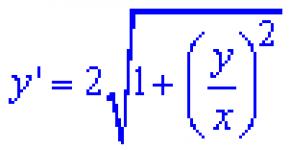Paruošti atsakymai į homogeninių diferencialinių lygčių pavyzdžius Daugelis studentų ieško pirmos eilės (dažniausiai mokant yra 1 eilės valdikliai), tuomet galėsite juos detaliai išanalizuoti. Tačiau prieš pereinant prie pavyzdžių svarstymo, rekomenduojame atidžiai perskaityti trumpą teorinę medžiagą.
Vadinamos P(x,y)dx+Q(x,y)dy=0 formos lygtys, kuriose funkcijos P(x,y) ir Q(x,y) yra tos pačios eilės vienarūšės funkcijos. vienalytė diferencialinė lygtis(ODR).

Vienalytės diferencialinės lygties sprendimo schema

1. Pirmiausia reikia pritaikyti pakaitalą y=z*x, kur z=z(x) yra nauja nežinoma funkcija (todėl pradinė lygtis redukuojama į diferencialinę lygtį su atskiriamais kintamaisiais).
2. Produkto išvestinė lygi y"=(z*x)"=z"*x+z*x"=z"*x+z arba diferencialuose dy=d(zx)=z*dx+ x*dz.
3. Toliau naują funkciją y ir jos išvestinę y" (arba dy) pakeičiame į DE su atskiriamais kintamaisiais x ir z atžvilgiu.
4. Išsprendę diferencialinę lygtį su atskiriamais kintamaisiais, atliekame atvirkštinį pokytį y=z*x, todėl z= y/x, ir gauname diferencialinės lygties bendrasis sprendinys (bendrasis integralas)..
5. Jei duota pradinė sąlyga y(x 0)=y 0, tada randame tam tikrą Koši uždavinio sprendimą. Teoriškai tai skamba lengvai, tačiau praktiškai ne visiems taip smagu spręsti diferencialines lygtis. Todėl, norėdami pagilinti žinias, pažvelkime į bendrus pavyzdžius. Nereikia daug ko išmokyti apie lengvas užduotis, todėl pereikime prie sudėtingesnių.

Pirmos eilės vienarūšių diferencialinių lygčių skaičiavimai

1 pavyzdys.

Sprendimas: Padalinkite dešinę lygties pusę iš kintamojo, kuris yra veiksnys šalia išvestinės. Dėl to mes pasiekiame 0 eilės vienalytė diferencialinė lygtis

Ir čia, ko gero, daugelis žmonių susidomėjo, kaip nustatyti vienalytės lygties funkcijos eiliškumą?
Klausimas yra gana aktualus, o atsakymas į jį yra toks:
dešinėje pusėje vietoj funkcijos ir argumento pakeičiame reikšmę t*x, t*y. Supaprastinant parametras „t“ gaunamas iki tam tikro laipsnio k, kuris vadinamas lygties tvarka. Mūsų atveju „t“ bus sumažintas, o tai atitinka 0 laipsnį arba vienalytės lygties nulinė eilė.
Toliau dešinėje pusėje galime pereiti prie naujo kintamojo y=zx; z=y/x.
Tuo pat metu nepamirškite išreikšti „y“ išvestinės per naujo kintamojo išvestinę. Pagal dalių taisyklę mes randame

Lygtys diferencialuoseįgaus formą

Atšaukiame bendrus terminus dešinėje ir kairėje pusėse ir pereiname prie diferencialinė lygtis su atskirtais kintamaisiais.

Integruokime abi DE puses

Tolesnių transformacijų patogumui konstantą iškart įrašome po logaritmu

Pagal logaritmų savybes gauta logaritminė lygtis yra lygiavertė šiai

Šis įrašas dar nėra sprendimas (atsakymas), reikia grįžti prie atlikto kintamųjų keitimo

Tokiu būdu jie randa bendras diferencialinių lygčių sprendimas. Jei atidžiai perskaitėte ankstesnes pamokas, tada sakėme, kad turėtumėte turėti galimybę laisvai naudoti lygčių su atskirtais kintamaisiais skaičiavimo schemą ir tokios lygtys turės būti skaičiuojamos sudėtingesniems nuotolinio valdymo pulto tipams.

2 pavyzdys. Raskite diferencialinės lygties integralą

Sprendimas: vienarūšių ir kombinuotų valdymo sistemų skaičiavimo schema dabar jums žinoma. Perkeliame kintamąjį į dešinę lygties pusę, taip pat išimame x 2 iš skaitiklio ir vardiklio kaip bendrą veiksnį

Taigi gauname homogeninę nulinės eilės diferencialinę lygtį.
Kitas žingsnis – įvesti kintamųjų z=y/x, y=z*x pakeitimą, kurį nuolat priminsime, kad įsimintumėte

Po to nuotolinio valdymo pultą įrašome diferencialais

Toliau mes transformuojame priklausomybę į diferencialinė lygtis su atskirtais kintamaisiais

ir mes tai sprendžiame integruodami.

Integralai paprasti, likusios transformacijos atliekamos pagal logaritmo savybes. Paskutinis žingsnis apima logaritmo atskleidimą. Galiausiai grįžtame prie pradinio pakeitimo ir įrašome jį į formą

Konstanta "C" gali turėti bet kokią reikšmę. Visi, kurie mokosi neakivaizdiniu būdu, turi problemų su tokio tipo lygtimis egzaminuose, todėl atidžiai peržiūrėkite ir atsiminkite skaičiavimo diagramą.

3 pavyzdys. Išspręskite diferencialinę lygtį

Sprendimas: Remiantis aukščiau pateikta metodika, išsprendžiamos tokio tipo diferencialinės lygtys įvedant naują kintamąjį. Perrašykime priklausomybę taip, kad išvestinė būtų be kintamojo

Be to, analizuodami dešinę pusę matome, kad fragmentas -ee yra visur ir žymi jį kaip naują nežinomą
z=y/x, y=z*x .
y išvestinės radimas

Atsižvelgdami į pakeitimą, formoje perrašome originalų DE

Supaprastiname identiškus terminus, o visus gautus terminus sumažiname iki DE su atskirtais kintamaisiais

Integruojant abi lygybės puses

prieiname prie sprendimo logaritmų pavidalu

Atskleidę rastas priklausomybes bendras diferencialinės lygties sprendimas

kuri į ją pakeitus pradinį kintamųjų pokytį įgauna formą

Čia C yra konstanta, kurią galima toliau nustatyti pagal Koši sąlygą. Jei Koši problema nenurodyta, ji įgauna savavališką tikrąją reikšmę.
Tai visa homogeninių diferencialinių lygčių skaičiavimo išmintis.

Šiame straipsnyje apžvelgsime homogeninių trigonometrinių lygčių sprendimo metodą.

Homogeninės trigonometrinės lygtys turi tokią pačią struktūrą kaip ir bet kurios kitos rūšies homogeninės lygtys. Leiskite man priminti antrojo laipsnio vienalyčių lygčių sprendimo metodą:

Panagrinėkime vienarūšes formos lygtis

Skiriamieji vienarūšių lygčių bruožai:

a) visi monomai turi tą patį laipsnį,

b) laisvas terminas lygus nuliui,

c) lygtyje yra galios su dviem skirtingais pagrindais.

Homogeninės lygtys sprendžiamos naudojant panašų algoritmą.

Norėdami išspręsti tokio tipo lygtį, mes padalijame abi lygties puses iš (gali būti padalinta iš arba iš)

Dėmesio! Dalijant dešinę ir kairę lygties puses iš išraiškos, kurioje yra nežinomasis, galite prarasti šaknis. Todėl reikia patikrinti, ar išraiškos, kuria dalijame abi lygties puses, šaknys yra pradinės lygties šaknys.

Jei taip, tada užrašome šią šaknį, kad vėliau jos nepamirštume, o tada padalijame išraišką iš to.

Apskritai, pirmas dalykas, kurį reikia padaryti sprendžiant bet kurią lygtį, kurios dešinėje pusėje yra nulis, yra pabandyti apskaičiuoti kairiąją lygties pusę bet kokiu prieinamu būdu. Ir tada kiekvieną veiksnį prilyginkite nuliui. Tokiu atveju šaknų tikrai neprarasime.

Taigi, atsargiai padalinkite kairę lygties pusę į išraiškos terminą pagal terminą. Mes gauname:

Sumažinkime antrosios ir trečiosios trupmenų skaitiklį ir vardiklį:

Pristatome pakaitalą:

Gauname kvadratinę lygtį:

Išspręskime kvadratinę lygtį, suraskime reikšmes ir grįžkime į pradinį nežinomybę.

Sprendžiant vienarūšes trigonometrines lygtis, reikia atsiminti keletą svarbių dalykų:

1. Manekeno terminą galima konvertuoti į sinuso ir kosinuso kvadratą naudojant pagrindinę trigonometrinę tapatybę:

2. Dvigubo argumento sinusas ir kosinusas yra antrojo laipsnio monomai – dvigubo argumento sinusą galima nesunkiai paversti sinuso ir kosinuso sandauga, o dvigubo argumento kosinusą – sinuso arba kosinuso kvadratu:

Pažvelkime į keletą vienarūšių trigonometrinių lygčių sprendimo pavyzdžių.

1 . Išspręskime lygtį:

Tai klasikinis pirmojo laipsnio vienalytės trigonometrinės lygties pavyzdys: kiekvieno monomio laipsnis lygus vienetui, pertraukos narys lygus nuliui.

Prieš dalydami abi lygties puses iš , turite patikrinti, ar lygties šaknys nėra pradinės lygties šaknys. Tikriname: if , then title="sin(x)0">, следовательно их сумма не равна нулю.!}

Padalinkime abi lygties puses iš .

Mes gauname:

, Kur

, Kur

Atsakymas: , Kur

2. Išspręskime lygtį:

Tai yra antrojo laipsnio vienalytės trigonometrinės lygties pavyzdys. Prisimename, kad jei galime apskaičiuoti kairę lygties pusę, patartina tai padaryti. Šioje lygtyje galime įdėti . Padarykime tai:

Pirmosios lygties sprendimas: , kur

Antroji lygtis yra vienalytė pirmojo laipsnio trigonometrinė lygtis. Norėdami tai išspręsti, padalykite abi lygties puses iš . Mes gauname:

Atsakymas: kur,

3. Išspręskime lygtį:

Kad ši lygtis „taptų“ vienalytė, paverčiame ją sandauga ir skaičių 3 pateikiame kaip sinuso ir kosinuso kvadratų sumą:

Perkelkime visus terminus į kairę, atidarykime skliaustus ir pateikime panašius terminus. Mes gauname:

Išskaidykime kairę pusę ir kiekvieną koeficientą nustatykime lygų nuliui:

Atsakymas: kur,

4 . Išspręskime lygtį:

Mes matome, ką galime išimti iš skliaustų. Padarykime tai:

Prilyginkime kiekvieną veiksnį nuliui:

Pirmosios lygties sprendimas:

Antroji populiacijos lygtis yra klasikinė antrojo laipsnio vienalytė lygtis. Lygties šaknys nėra pradinės lygties šaknys, todėl abi lygties puses padalijame iš:

Pirmosios lygties sprendimas:

Antrosios lygties sprendimas.

Norėdami išspręsti homogeninę 1-osios eilės diferencialinę lygtį, naudokite pakaitalą u=y/x, tai yra, u yra nauja nežinoma funkcija, priklausanti nuo x. Taigi y=ux. Išvestinę y’ randame naudodami sandaugų diferenciacijos taisyklę: y’=(ux)’=u’x+x’u=u’x+u (kadangi x’=1). Kitai žymėjimo formai: dy = udx + xdu. Po pakeitimo lygtį supaprastiname ir gauname lygtį su atskiriamais kintamaisiais.

1 eilės vienarūšių diferencialinių lygčių sprendimo pavyzdžiai.

1) Išspręskite lygtį

Patikriname, ar ši lygtis yra vienalytė (žr. Kaip nustatyti vienalytę lygtį). Įsitikinus atliekame pakeitimą u=y/x, iš kurio y=ux, y’=(ux)’=u’x+x’u=u’x+u. Pakaitalas: u’x+u=u(1+ln(ux)-lnx). Kadangi sandaugos logaritmas lygus logaritmų sumai, ln(ux)=lnu+lnx. Iš čia

u'x+u=u(1+lnu+lnx-lnx). Atvedus panašius terminus: u’x+u=u(1+lnu). Dabar atidarykite skliaustus

u'x+u=u+u·lnu. Abiejose pusėse yra u, taigi u’x=u·lnu. Kadangi u yra x funkcija, u’=du/dx. Pakeiskime

Gavome lygtį su atskiriamais kintamaisiais. Kintamuosius atskiriame abi dalis padaugindami iš dx ir padalydami iš x·u·lnu, su sąlyga, kad sandauga x·u·lnu≠0

Integruokime:

Kairėje pusėje yra stalo integralas. Dešinėje - pakeičiame t=lnu, iš kur dt=(lnu)’du=du/u

ln│t│=ln│x│+C. Bet jau aptarėme, kad tokiose lygtyse patogiau vietoj C imti ln│C│. Tada

ln│t│=ln│x│+ln│C│. Pagal logaritmų savybę: ln│t│=ln│Сx│. Taigi t = Cx. (pagal sąlygą, x>0). Atėjo laikas atlikti atvirkštinį pakeitimą: lnu=Cx. Ir dar vienas atvirkštinis pakeitimas:

Pagal logaritmų savybę:

Tai yra bendrasis lygties integralas.

Primename sandaugos x·u·lnu≠0 (taigi x≠0,u≠0, lnu≠0, iš kur u≠1) sąlygą. Bet iš sąlygos x≠0 lieka u≠1, taigi x≠y. Akivaizdu, kad y=x (x>0) yra įtraukti į bendrą sprendimą.

2) Raskite lygties y’=x/y+y/x dalinį integralą, tenkinantį pradines sąlygas y(1)=2.

Pirmiausia patikriname, ar ši lygtis yra vienalytė (nors terminų y/x ir x/y buvimas jau netiesiogiai tai rodo). Tada atliekame pakeitimą u=y/x, iš kurio y=ux, y’=(ux)’=u’x+x’u=u’x+u. Gautas išraiškas pakeičiame į lygtį:

u'x+u=1/u+u. Supaprastinkime:

u'x=1/u. Kadangi u yra x funkcija, u’=du/dx:

Gavome lygtį su atskiriamais kintamaisiais. Norėdami atskirti kintamuosius, padauginame abi puses iš dx ir u ir padalijame iš x (x≠0 pagal sąlygą, taigi ir u≠0, o tai reiškia, kad sprendinių nėra).

Integruokime:

o kadangi abiejose pusėse yra lentelės integralai, iš karto gauname

Atliekame atvirkštinį keitimą:

Tai yra bendrasis lygties integralas. Naudojame pradinę sąlygą y(1)=2, tai yra, gautame sprendinyje pakeičiame y=2, x=1:

3) Raskite homogeninės lygties bendrąjį integralą:

(x²-y²)dy-2xydx=0.

Pakeitimas u=y/x, iš kur y=ux, dy=xdu+udx. Pakeiskime:

(x²-(ux)²)(xdu+udx)-2ux²dx=0. Iš skliaustų išimame x² ir iš jo padalijame abi dalis (jei x≠0):

x²(1-u²)(xdu+udx)-2ux²dx=0

(1-u²)(xdu+udx)-2udx=0. Atidarykite skliaustus ir supaprastinkite:

xdu-u²xdu+udx-u³dx-2udx=0,

xdu-u²xdu-u³dx-udx=0. Sugrupuojame terminus su du ir dx:

(x-u²x)du-(u³+u)dx=0. Išimkime įprastus veiksnius iš skliaustų:

x(1-u²)du-u(u²+1)dx=0. Mes atskiriame kintamuosius:

x(1-u²)du=u(u²+1)dx. Norėdami tai padaryti, padalijame abi lygties puses iš xu(u²+1)≠0 (atitinkamai pridedame reikalavimus x≠0 (jau pažymėta), u≠0):

Integruokime:

Dešinėje lygties pusėje yra lentelės integralas, o kairėje pusėje esančią racionaliąją trupmeną išskaidome į paprastus veiksnius:

(arba antrame integrale, vietoj diferencialo ženklo pakeitimo buvo galima padaryti keitimą t=1+u², dt=2udu - kam patinka kuris būdas geresnis). Mes gauname:

Pagal logaritmų savybes:

Atvirkštinis pakeitimas

Primename sąlygą u≠0. Taigi y≠0. Kai C=0 y=0, tai reiškia, kad nėra sprendinių praradimo, o y=0 įtraukiamas į bendrąjį integralą.

komentuoti

Galite gauti sprendimą, parašytą kita forma, jei paliksite terminą su x kairėje:

Integralinės kreivės geometrinė reikšmė šiuo atveju yra apskritimų šeima, kurių centrai yra Oy ašyje ir eina per pradžią.

Savikontrolės užduotys:

1) (x²+y²)dx-xydy=0

1) Patikriname, ar lygtis yra vienalytė, po to atliekame pakeitimą u=y/x, iš kur y=ux, dy=xdu+udx. Pakeiskite sąlygą: (x²+x²u²)dx-x²u(xdu+udx)=0. Abi lygties puses padalijus iš x²≠0, gauname: (1+u²)dx-u(xdu+udx)=0. Taigi dx+u²dx-xudu-u²dx=0. Supaprastinus, turime: dx-xudu=0. Taigi xudu=dx, udu=dx/x. Integruokime abi dalis:

Homogeniškas

Šioje pamokoje apžvelgsime vadinamąją pirmos eilės vienarūšės diferencialinės lygtys. Kartu su atskiriamas lygtis Ir tiesinės nehomogeninės lygtysŠio tipo nuotolinio valdymo pultas randamas beveik bet kuriame bandomajame darbe difuzorių tema. Jei atėjote į puslapį iš paieškos variklio arba nesate labai įsitikinę, kad supratote diferencialines lygtis, pirmiausia primygtinai rekomenduoju atlikti įvadinę pamoką šia tema - Pirmosios eilės diferencialinės lygtys. Faktas yra tas, kad daugelis vienarūšių lygčių sprendimo principų ir taikomų metodų bus visiškai tokie patys kaip ir paprasčiausioms lygtims su atskiriamais kintamaisiais.

Kuo skiriasi vienarūšės diferencialinės lygtys ir kitų tipų diferencialinės lygtys? Lengviausias būdas iš karto tai paaiškinti konkrečiu pavyzdžiu.

1 pavyzdys

Sprendimas:
Ką Pirmiausia priimant sprendimą turėtų būti išanalizuotas bet koks diferencialinė lygtis Pirmas užsakymas? Pirmiausia reikia patikrinti, ar galima iš karto atskirti kintamuosius naudojant „mokyklinius“ veiksmus? Paprastai ši analizė atliekama mintyse arba bandant atskirti kintamuosius juodraštyje.

Šiame pavyzdyje kintamųjų negalima atskirti(galite pabandyti mesti terminus iš dalies į dalį, iškelti veiksnius iš skliaustų ir pan.). Beje, šiame pavyzdyje faktas, kad kintamieji negali būti skaidomi, yra gana akivaizdus dėl daugiklio buvimo.

Kyla klausimas: kaip išspręsti šią išsklaidytą problemą?

Reikia patikrinti ir Ar ši lygtis nėra vienalytė?? Patikrinimas yra paprastas, o patį patikrinimo algoritmą galima suformuluoti taip:

Į pradinę lygtį:

vietoj mes pakeičiame, vietoj mes pakeičiame, mes neliečiame išvestinės:

Lambda raidė yra sąlyginis parametras, ir čia ji atlieka tokį vaidmenį: jei dėl transformacijų galima „sunaikinti“ VISAS lambdas ir gauti pirminę lygtį, tada ši diferencialinė lygtis yra vienalytis.

Akivaizdu, kad lambdas iš karto redukuoja eksponentas:

Dabar dešinėje pusėje išimame lambda iš skliausteliuose:

ir padalykite abi dalis iš tos pačios lambda:

Kaip rezultatas Visi Lambdai dingo kaip sapnas, kaip ryto rūkas, ir gavome pirminę lygtį.

Išvada:Ši lygtis yra vienalytė

Kaip išspręsti vienalytę diferencialinę lygtį?

Turiu labai gerų naujienų. Absoliučiai visas vienarūšes lygtis galima išspręsti naudojant vieną (!) standartinį pakaitalą.

„Žaidimo“ funkcija turėtų būti pakeisti dirbti tam tikra funkcija (taip pat priklauso nuo „x“) ir "x":

Jie beveik visada trumpai rašo:

Išsiaiškiname, į ką darinys pavirs tokiu pakeitimu, naudojame produkto diferenciacijos taisyklę. Jei tada:

Į pradinę lygtį pakeičiame:

Ką duos toks pakaitalas? Po šio pakeitimo ir supaprastinimų mes garantuotas gauname lygtį su atskiriamais kintamaisiais. PRISIMINTI kaip pirmoji meilė :) ir, atitinkamai, .

Po pakeitimo atliekame maksimalius supaprastinimus:

Kadangi funkcija priklauso nuo „x“, jos išvestinę galima parašyti kaip standartinę trupmeną: .
Taigi:

Mes atskiriame kintamuosius, o kairėje pusėje reikia rinkti tik „te“, o dešinėje - tik „x“:

Kintamieji yra atskirti, integruokime:


Pagal mano pirmąjį techninį patarimą iš straipsnio Pirmosios eilės diferencialinės lygtys, daugeliu atvejų konstantą patartina „suformuluoti“ logaritmo forma.

Kai lygtis buvo integruota, turime atlikti atvirkštinis pakeitimas, jis taip pat yra standartinis ir unikalus:
Jei tada
Tokiu atveju:

18-19 atvejų iš 20 homogeninės lygties sprendinys rašomas bendruoju integralu.

Atsakymas: bendras integralas:

Kodėl atsakymas į vienalytę lygtį beveik visada pateikiamas bendrojo integralo forma?
Daugeliu atvejų neįmanoma aiškiai išreikšti „žaidimo“ (gauti bendrą sprendimą), o jei įmanoma, tada dažniausiai bendras sprendimas pasirodo gremėzdiškas ir gremėzdiškas.

Taigi, pavyzdžiui, nagrinėjamame pavyzdyje, bendrą sprendimą galima gauti pasveriant logaritmus abiejose bendrojo integralo pusėse:

- Na, viskas gerai. Nors, jūs turite pripažinti, jis vis dar yra šiek tiek kreivas.

Beje, šiame pavyzdyje ne visai „padoriai“ užrašiau bendrąjį integralą. Tai ne klaida, bet „geru“ stiliumi primenu, kad bendras integralas dažniausiai rašomas forma . Norėdami tai padaryti, iškart po lygties integravimo konstanta turėtų būti užrašoma be logaritmo (čia yra taisyklės išimtis!):

Ir po atvirkštinio pakeitimo gaukite bendrąjį integralą „klasikine“ forma:

Gautą atsakymą galima patikrinti. Norėdami tai padaryti, turite atskirti bendrąjį integralą, tai yra, rasti netiesiogiai nurodytos funkcijos išvestinė:

Mes atsikratome trupmenų, padaugindami kiekvieną lygties pusę iš:

Gauta pradinė diferencialinė lygtis, o tai reiškia, kad sprendimas buvo rastas teisingai.

Patartina visada patikrinti. Tačiau vienarūšės lygtys nemalonios tuo, kad paprastai sunku patikrinti jų bendruosius integralus – tam reikia labai labai padoraus diferencijavimo technikos. Nagrinėjamame pavyzdyje patikros metu jau reikėjo rasti ne pačius paprasčiausius išvestinius (nors pats pavyzdys gana paprastas). Jei galite tai patikrinti, patikrinkite!

Toliau pateiktą pavyzdį turite išspręsti patys, kad galėtumėte patogiai naudotis veiksmų algoritmu:

2 pavyzdys

Patikrinkite lygties homogeniškumą ir raskite jos bendrąjį integralą.

Parašykite atsakymą į formą, patikrinkite.

Čia taip pat pasirodė gana paprastas patikrinimas.

O dabar žadėtas svarbus dalykas, paminėtas pačioje temos pradžioje,
Paryškinsiu juodomis raidėmis:

Jei transformacijų metu „iš naujo nustatome“ daugiklį (ne konstanta)į vardiklį, tada RIZIKUOJAME prarasti sprendimus!

Ir iš tikrųjų su tuo susidūrėme pirmame pavyzdyje įvadinė pamoka apie diferencialines lygtis. Sprendžiant lygtį, „y“ pasirodė vardiklyje: , bet akivaizdu, kad tai yra DE sprendimas ir dėl nevienodos transformacijos (dalybos) yra visos galimybės jį prarasti! Kitas dalykas yra tai, kad jis buvo įtrauktas į bendrą sprendimą nuline konstantos verte. Taip pat galima nepaisyti vardiklio „X“ nustatymo iš naujo, nes netenkina originalaus difuzoriaus.

Panaši istorija su trečiąja tos pačios pamokos lygtimi, kurios sprendimo metu „nukritome“ į vardiklį. Griežtai tariant, čia reikėjo patikrinti, ar šis difuzorius yra sprendimas? Juk taip yra! Bet net ir čia „viskas pasirodė gerai“, nes ši funkcija buvo įtraukta į bendrą integralą adresu .

Ir jei tai dažnai veikia su „atskiriamomis“ lygtimis, tai su homogeniniais ir kai kuriais kitais difuzoriais tai gali neveikti. Labai tikėtina.

Išanalizuokime šioje pamokoje jau išspręstas problemas: in 1-2 pavyzdžiai„Reset“ X taip pat pasirodė saugu, nes yra ir , todėl iš karto aišku, kad tai negali būti sprendimas. Be to, į 2 pavyzdys pasirodė esąs vardiklyje, ir čia rizikavome prarasti funkciją, kuri akivaizdžiai tenkina lygtį . Tačiau ir čia „praėjo“, nes... į bendrąjį integralą jis įėjo esant nulinei konstantos reikšmei.

Bet, žinoma, tyčia sukūriau „linksmas progas“, ir tai nėra faktas, kad praktikoje pasitaikys būtent šios:

3 pavyzdys

Išspręskite diferencialinę lygtį

Argi ne paprastas pavyzdys? ;-)

Sprendimas:šios lygties homogeniškumas yra akivaizdus, ​​bet vis tiek - pirmame žingsnyje Mes VISADA tikriname, ar įmanoma atskirti kintamuosius. Mat lygtis taip pat yra vienalytė, tačiau joje esantys kintamieji lengvai atskiriami. Taip, yra keletas!

Patikrinę, ar nėra „atskiriamumo“, pakeičiame ir kiek įmanoma supaprastiname lygtį:

Atskirame kintamuosius, surenkame „te“ kairėje ir „x“ dešinėje:

Ir čia STOP. Dalindami iš rizikuojame prarasti dvi funkcijas vienu metu. Nuo , tai yra šios funkcijos:

Akivaizdu, kad pirmoji funkcija yra lygties sprendimas . Patikriname antrąjį – jo darinį taip pat pakeičiame į mūsų difuzorių:

– gaunama teisinga lygybė, o tai reiškia, kad funkcija taip pat yra sprendimas.

IR rizikuojame prarasti šiuos sprendimus.

Be to, vardiklis pasirodė esąs „X“, taigi būtinai patikrink, nėra pradinės diferencialinės lygties sprendimas. Ne, nėra.

Įsidėmėkime visa tai ir tęskime:

Turiu pasakyti, kad man pasisekė su kairiosios pusės integralu, gali būti daug blogiau.

Dešinėje pusėje surenkame vieną logaritmą ir nusimetame pančius:

O dabar tik atvirkštinis pakeitimas:

Padauginkime visus terminus iš:

Dabar turėtumėte patikrinti - ar „pavojingi“ sprendiniai buvo įtraukti į bendrąjį integralą. Taip, abu sprendiniai buvo įtraukti į bendrąjį integralą nuline konstantos verte: , todėl jų papildomai nurodyti nereikia atsakyti:

bendras integralas:

Apžiūra. Net ne išbandymas, o grynas malonumas :)

Gauta pradinė diferencialinė lygtis, o tai reiškia, kad sprendimas buvo rastas teisingai.

Norėdami tai išspręsti patys:

4 pavyzdys

Atlikite homogeniškumo testą ir išspręskite diferencialinę lygtį

Patikrinkite bendrąjį integralą diferencijuodami.

Visas sprendimas ir atsakymas pamokos pabaigoje.

Pažvelkime į keletą tipiškesnių pavyzdžių:

5 pavyzdys

Išspręskite diferencialinę lygtį

SprendimasĮprasim jį projektuoti kompaktiškiau. Pirmiausia mintyse arba juodraštyje įsitikiname, kad kintamųjų čia negalima atskirti, o po to atliekame homogeniškumo testą – tai paprastai neatliekama galutiniame juodraštyje. (nebent specialiai reikalaujama). Taigi sprendimas beveik visada prasideda įrašu: „ Ši lygtis yra vienalytė, pakeiskime: ...».

Pakeitimas, ir einame pramintu keliu:

„X“ čia tinka, bet kaip dėl kvadratinio trinalio? Kadangi jis nėra išskaidomas į veiksnius: , tada mes tikrai neprarandame sprendimų. Visada būtų taip! Kairėje pusėje pasirinkite visą kvadratą ir integruokite:

Čia nėra ką supaprastinti, taigi ir atvirkštinis pakeitimas:

Atsakymas: bendras integralas:

Šis nepriklausomo sprendimo pavyzdys:

6 pavyzdys

Išspręskite diferencialinę lygtį

Atrodytų, lygtys panašios, bet ne – didelis skirtumas ;)

O dabar linksmybės prasideda! Pirmiausia išsiaiškinkime, ką daryti, jei vienalytė lygtis pateikiama su paruoštais diferencialais:

7 pavyzdys

Išspręskite diferencialinę lygtį

Tai labai įdomus pavyzdys, visas trileris!

Sprendimas: jei homogeninėje lygtyje yra paruoštų diferencialų, tada ją galima išspręsti modifikuotu pakeitimu:

Bet aš nerekomenduoju naudoti tokio pakeitimo, nes tai bus Didžioji Kinijos diferencialų siena, kur reikia akies ir akies. Techniniu požiūriu naudingiau pereiti prie „brūkšninio“ išvestinio žymėjimo; tam mes padalijame abi lygties puses iš:

Ir štai mes jau padarėme „pavojingą“ transformaciją! Nulinis skirtumas atitinka lygiagrečių ašiai tiesių linijų šeimą. Ar jie yra mūsų DU šaknys? Pakeiskime pradinę lygtį:

Ši lygybė galioja, jei, ty dalindami iš rizikuojame prarasti sprendimą, ir mes jį praradome- Nuo tada, kai tai nebetenkina gautą lygtį .

Reikia pažymėti, kad jei mes iš pradžių buvo pateikta lygtis , tada apie šaknį nebūtų nė kalbos. Bet mes jį turime ir laiku pagavome.

Tęsiame sprendimą su standartiniu pakeitimu:
:

Pakeitę lygtį kiek įmanoma supaprastiname:

Mes atskiriame kintamuosius:

Ir čia vėl STOP: dalindami iš rizikuojame prarasti dvi funkcijas. Nuo , tai yra šios funkcijos:

Akivaizdu, kad pirmoji funkcija yra lygties sprendimas . Patikriname antrąjį – taip pat pakeičiame jo darinį:

– gavo tikroji lygybė, o tai reiškia, kad funkcija taip pat yra diferencialinės lygties sprendimas.

O dalindami iš rizikuojame prarasti šiuos sprendimus. Tačiau jie gali patekti į bendrąjį integralą. Bet jie gali ir neįeiti

Atsižvelkime į tai ir integruokime abi dalis:

Kairiosios pusės integralas išsprendžiamas standartiniu būdu naudojant išryškinant ištisą aikštę, bet daug patogiau naudoti difuzoriuose neapibrėžtųjų koeficientų metodas:

Naudodami neapibrėžtų koeficientų metodą, integrandą išplečiame į elementariųjų trupmenų sumą:


Taigi:

Integralų paieška:

– kadangi braižome tik logaritmus, tai ir konstantą stumiame po logaritmu.

Prieš pakeičiant vėl supaprastinant viską, ką galima supaprastinti:

Grandinių nustatymas iš naujo:

Ir atvirkštinis pakeitimas:

Dabar prisiminkime apie „pamestus daiktus“: sprendimas buvo įtrauktas į bendrąjį integralą, bet „praskriejo pro kasą“, nes pasirodė vardiklis. Todėl atsakyme jam suteikiama atskira frazė, ir taip - nepamirškite apie prarastą sprendimą, kuris, beje, taip pat pasirodė žemiau.

Atsakymas: bendras integralas: . Daugiau sprendimų:

Čia nėra taip sunku išreikšti bendrą sprendimą:
, bet tai jau demonstravimas.

Tačiau patogu patikrinti. Raskime išvestinę:

ir pakaitalas kairėje lygties pusėje:

– kaip rezultatas, buvo gauta dešinioji lygties pusė, kurią ir reikėjo patikrinti.

Dabar ieškojimas su šaknimis taip pat yra dažnas ir labai klastingas atvejis:

8 pavyzdys

Išspręskite diferencialinę lygtį

Sprendimas: Žodžiu įsitikinkite, kad lygtis yra vienalytė, ir pirmąją meilę pakeiskite pirmine lygtimi:

Ir jau čia mūsų laukia pavojus. Esmė ta, kad šį faktą labai lengva pamiršti:

Laimingos reklamos!

Sprendimai ir atsakymai:

2 pavyzdys: Sprendimas: Patikrinkime lygties homogeniškumą, šiuo tikslu pradinėje lygtyje vietoj pakeiskime , ir vietoj pakeiskime:

Dėl to gaunama pradinė lygtis, o tai reiškia, kad ši DE yra vienalytė.

Pirmos eilės vienalytė diferencialinė lygtis yra formos lygtis
, kur f yra funkcija.

Kaip nustatyti homogeninę diferencialinę lygtį

Norint nustatyti, ar pirmos eilės diferencialinė lygtis yra vienalytė, reikia įvesti konstantą t ir y pakeisti ty ir x tx: y → ty, x → tx. Jei t atšaukia, tada tai vienalytė diferencialinė lygtis. Išvestinė y′ dėl šios transformacijos nekinta.
.

Pavyzdys

Nustatykite, ar duotoji lygtis yra vienalytė

Sprendimas

Pakeičiame y → ty, x → tx.


Padalinkite iš t 2 .

.
Lygtyje nėra t. Todėl tai yra vienalytė lygtis.

Homogeninės diferencialinės lygties sprendimo būdas

Pirmos eilės vienalytė diferencialinė lygtis redukuojama į lygtį su atskiriamais kintamaisiais, naudojant pakaitalą y = ux. Parodykime. Apsvarstykite lygtį:
(i)
Padarykime pakaitalą:
y = ux,
kur u yra x funkcija. Atskirkite x atžvilgiu:
y′ =
Pakeiskite pradinę lygtį (i).
,
,
(ii) .
Atskirkime kintamuosius. Padauginkite iš dx ir padalykite iš x ( f(u) – u ).

Prie f (u) – u ≠ 0 ir x ≠ 0 mes gauname:

Integruokime:

Taigi mes gavome bendrąjį lygties integralą (i) kvadratais:

Integracijos konstantą C pakeisime C, Tada

Modulio ženklą praleiskime, nes norimą ženklą lemia konstantos C ženklo pasirinkimas. Tada bendras integralas įgis tokią formą:

Toliau turėtume apsvarstyti atvejį f (u) – u = 0.
Jei ši lygtis turi šaknis, tai jos yra lygties sprendimas (ii). Kadangi Eq. (ii) nesutampa su pradine lygtimi, tuomet turėtumėte įsitikinti, kad papildomi sprendiniai atitinka pradinę lygtį (i).

Kai mes transformacijų procese bet kurią lygtį padalijame iš kokios nors funkcijos, kurią žymime kaip g (x, y), tada tolimesnės transformacijos galioja g (x, y) ≠ 0. Todėl atvejis g turėtų būti nagrinėjamas atskirai (x, y) = 0.

Vienalytės pirmos eilės diferencialinės lygties sprendimo pavyzdys

Išspręskite lygtį

Sprendimas

Patikrinkime, ar ši lygtis yra vienalytė. Pakeičiame y → ty, x → tx. Šiuo atveju y′ → y′.
,
,
.
Sutrumpiname t.

Konstanta t sumažėjo. Todėl lygtis yra vienalytė.

Pakeičiame y = ux, kur u yra x funkcija.
y′ = (ux) ′ = u′ x + u (x) ′ = u′ x + u
Pakeiskite pradinę lygtį.
,
,
,
.
Kai x ≥ 0 , |x| = x. Kai x ≤ 0 , |x| = - x . Rašome |x| = x reiškia, kad viršutinis ženklas reiškia reikšmes x ≥ 0 , o apatinė - į reikšmes x ≤ 0 .
,
Padauginkite iš dx ir padalykite iš .

Kai u 2 - 1 ≠ 0 mes turime:

Integruokime:

Lenteliniai integralai,
.

Taikome formulę:
(a + b) (a - b) = a 2 - b 2.
Padėkime a = u, .
.
Paimkime abi puses modulio ir logaritmizavimo,
.
Iš čia
.

Taigi mes turime:
,
.
Modulio ženklą praleidžiame, nes norimas ženklas užtikrinamas pasirinkus konstantos C ženklą.

Padauginkite iš x ir pakeiskite ux = y.
,
.
Kvadratu.
,
,
.

Dabar apsvarstykite atvejį, u 2 - 1 = 0 .
Šios lygties šaknys
.
Nesunku patikrinti, ar funkcijos y = x atitinka pradinę lygtį.

Atsakymas

,
,
.

Nuorodos:
N.M. Gunteris, R.O. Kuzminas, Aukštosios matematikos uždavinių rinkinys, „Lan“, 2003 m.